已知二次函数f(x)=ax2+bx+c,当x∈(-∞,-2)∪(0,+∞)时f(x)>0,当x∈(-2,0)时,f(x)<0且对任意x∈R,不等式f(x)≥(a-1)x-1恒成立.(1)求函数f(x)的解析式;(2)f(x)>m恒成立,求m的取值范围.
解:(1)∵二次函数f(x)=ax
2+bx+c,当x∈(-∞,-2)∪(0,+∞)时f(x)>0,当x∈(-2,0)时,f(x)<0
∴ax
2+bx+c=0的两个根为-2和0
将-2和0代入方程ax
2+bx+c=0可得c=0,b=2a
∵对任意x∈R,不等式f(x)≥(a-1)x-1恒成立
∴ax
2+2ax≥(a-1)x-1恒成立
即ax
2+(a+1)x+1≥0恒成立
∴
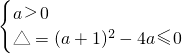
解得a=1,b=2
∴f(x)=x
2+2x
(2)∵f(x)>m恒成立,
∴f(x)
min=-1>m
即m的取值范围(-∞,-1)
分析:(1)先根据题意得到ax
2+bx+c=0的两个根为-2和0,可求出a与b的关系以及c的值,然后根据对任意x∈R,不等式f(x)≥(a-1)x-1恒成立建立不等关系,解之即可;
(2)欲使f(x)>m恒成立,即使f(x)
min>m即可,然后求出f(x)的最小值即可.
点评:本题主要考查了函数恒成立问题,以及二次函数的性质,同时考查了等价转化的思想和计算能力,属于中档题.

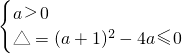 解得a=1,b=2
解得a=1,b=2
