
【题目】记不等式组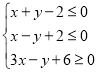 ,表示的平面区域为
,表示的平面区域为![]() .下面给出的四个命题:
.下面给出的四个命题:![]() ;
;![]() ;
;![]() ;
;![]() 其中真命题的是:
其中真命题的是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由约束条件作出可行域,利用目标函数的几何意义求解z=x+y,z1=2x﹣y,z2![]() ,z3=x2+y2,的范围,判断命题的真假即可.
,z3=x2+y2,的范围,判断命题的真假即可.
实数x,y满足 ,由约束条件作出可行域为D,如图阴影部分,
,由约束条件作出可行域为D,如图阴影部分,
A(﹣2,0),B(0,2),C(﹣1,3),z=x+y经过可行域的点A及直线BC时分别取得最值,可得:z∈[﹣2,2],所以![]() 错误;
错误;
z1=2x﹣y经过可行域的B、C时分别取得最值,可得:z1∈[﹣5,﹣2],所以![]() 正确;
正确;
z2![]() ,它的几何意义是可行域内的点与(1,﹣1)连线的斜率,
,它的几何意义是可行域内的点与(1,﹣1)连线的斜率,
可得:DA的斜率是最大值为:![]() ;
;
BD的斜率取得最小值为:![]() ;z2∈[
;z2∈[![]() ,
,![]() ];所以
];所以![]() 错误;
错误;
z3=x2+y2,它的几何意义是可行域内的点与(0,0)连线的距离的平方,
最小值为原点到直线y=x+2的距离的平方:(![]() )2
)2![]() ,最大值为OC的平方:(﹣1﹣0)2+(3﹣0)2=10,z3∈[
,最大值为OC的平方:(﹣1﹣0)2+(3﹣0)2=10,z3∈[![]() ,10].所以
,10].所以![]() 正确;
正确;
故选:C.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若整数![]() 满足:
满足:![]() ,称
,称![]() 为离实数
为离实数![]() 最近的整数,记作
最近的整数,记作![]() .给出函数
.给出函数![]() 的四个命题:
的四个命题:
①函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ;
;
②函数![]() 是周期函数,最小正周期为
是周期函数,最小正周期为![]() ;
;
③函数![]() 在
在![]() 上是增函数;
上是增函数;
④函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
其中所有的正确命题的序号为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,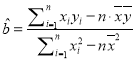 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
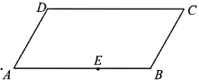
【题目】下图是一块平行四边形园地![]() ,经测量,
,经测量,![]()
![]() .拟过线段
.拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计直路的宽度),将该园地分为面积之比为
的边上,不计直路的宽度),将该园地分为面积之比为![]() 的左,右两部分分别种植不同花卉.设
的左,右两部分分别种植不同花卉.设![]() (单位:m).
(单位:m).
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)试确定点![]() 的位置,使直路
的位置,使直路![]() 的长度最短.
的长度最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com