
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
【答案】(1) 曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的普通方程为
的普通方程为![]() ; (2)
; (2) ![]()
【解析】
(1)由极坐标与直角坐标的互化公式和参数方程与普通方程的互化,即可求解曲线的直角坐标方程和直线的普通方程;
(2)把![]() 的参数方程代入抛物线方程中,利用韦达定理得
的参数方程代入抛物线方程中,利用韦达定理得![]() ,
,![]() ,可得到
,可得到![]() ,根据因为
,根据因为![]() ,
,![]() ,
,![]() 成等比数列,列出方程,即可求解.
成等比数列,列出方程,即可求解.
(1)由题意,曲线![]() 的极坐标方程可化为
的极坐标方程可化为![]() ,
,
又由![]() ,可得曲线
,可得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
由直线![]() 的参数方程为
的参数方程为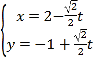 (
(![]() 为参数),消去参数
为参数),消去参数![]() ,得
,得![]() ,
,
即直线![]() 的普通方程为
的普通方程为![]() ;
;
(2)把![]() 的参数方程
的参数方程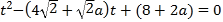 代入抛物线方程中,得
代入抛物线方程中,得![]() ,
,
由![]() ,设方程的两根分别为
,设方程的两根分别为![]() ,
,![]() ,
,
则![]() ,
,![]() ,可得
,可得![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,![]() 成等比数列,所以
成等比数列,所以![]() ,即
,即![]() ,
,
则![]() ,解得解得
,解得解得![]() 或
或![]() (舍),
(舍),
所以实数![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为![]() |OB|.
|OB|.
(1)求椭圆C的方程;
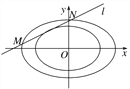
(2)如图,若椭圆![]() ,椭圆
,椭圆![]() ,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]()
![]() =
=![]() (
(![]() >0),过点
>0),过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线![]() 与曲线C相交于A,B两点.
与曲线C相交于A,B两点.
(Ⅰ)写出曲线C的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
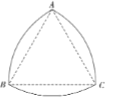
【题目】勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )
A.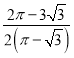 B.
B.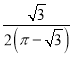
C.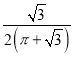 D.
D.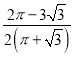
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
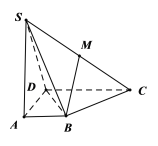
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)![]() 为
为![]() 中点,在四边形
中点,在四边形![]() 所在的平面内是否存在一点
所在的平面内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求三角形
,若存在,求三角形![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,若点A为函数
,若点A为函数![]() 上的任意一点,点B为函数
上的任意一点,点B为函数![]() 上的任意一点.
上的任意一点.
(1)求A,B两点之间距离的最小值;
(2)若A,B为函数![]() 与函数
与函数![]() 公切线的两个切点,求证:这样的点B有且仅有两个,且满足条件的两个点B的横坐标互为倒数.
公切线的两个切点,求证:这样的点B有且仅有两个,且满足条件的两个点B的横坐标互为倒数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年将在日本东京举办第
年将在日本东京举办第![]() 届夏季奥林匹克运动会,简称为“奥运会”,为了解不同年龄的人对“奥运会”的关注程度,某机构随机抽取了年龄在
届夏季奥林匹克运动会,简称为“奥运会”,为了解不同年龄的人对“奥运会”的关注程度,某机构随机抽取了年龄在![]() 岁之间的
岁之间的![]() 人进行调查,经统计,“年轻人”与“中老年人”的人数之比为
人进行调查,经统计,“年轻人”与“中老年人”的人数之比为![]() .
.
关注 | 不关注 | 合计 | |
年轻人 |
| ||
中老年人 | |||
合计 |
|
|
|
(1)根据已知条件完成上面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为是否关注“奥运会”与年龄段有关;
的把握认为是否关注“奥运会”与年龄段有关;
(2)现采用分层抽样的方法从中老年人中选取![]() 人进行问卷调查.若再从这
人进行问卷调查.若再从这![]() 人中选取
人中选取![]() 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的![]() 人中至少有
人中至少有![]() 人关注奥运会”的概率.
人关注奥运会”的概率.
附参考公式: ,其中
,其中![]() 临界值表:
临界值表:
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com