解:(1)由f (3+x)=f (1-x),可得f (2+x)=f(2-x),
∴y=f (x)的对称轴为x=2.…
当2<x
1<x
2时,f (x
1)<f (x
2); 当2<x
2<x
1时,f (x
2)<f (x
1).
∴y=f (x)在(2,+∝)上为增函数,在(-∞,2)上为减函数.…
(2)由f(cos
2θ+2m
2+2)<f(sinθ+m
2-3m-2),可得|cos
2θ+2m
2|<|sinθ+m
2-3m-4|,
即m
2-3m-4+sinθ>cos
2θ+2m
2(i),或m
2-3m-4+sinθ<-cos
2θ-2m
2(ii)恒成立.…
由(i)得m
2+3m+4<-cos
2θ+sinθ=(sinθ+

)
2-

恒成立,∴m
2+3m+4<-

,
故 4m
2+12m+21<0恒成立,m无解.…
由(ii) 得3m
2-3m-4<-cos
2θ-sinθ=(sinθ-

)
2-

恒成立,可得3m
2-3m-4<-

,
即 12m
2-12m-11<0,解得
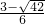
<m<
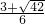
.…
分析:(1)由条件可得y=f (x)的对称轴为x=2,当2<x
1<x
2时,f (x
1)<f (x
2); 当2<x
2<x
1时,f (x
2)<f (x
1),由此可得结论.
(2)由f(cos
2θ+2m
2+2)<f(sinθ+m
2-3m-2),可得|cos
2θ+2m
2|<|sinθ+m
2-3m-4|,即m
2-3m-4+sinθ>cos
2θ+2m
2(i),或m
2-3m-4+sinθ<-cos
2θ-2m
2(ii)恒成立.由(i)得求得m的范围,由(ii)求得m的范围,再把这2个m的范围取并集,即得所求.
点评:本题主要函数的单调性的判断和证明,函数的恒成立问题,属于基础题.

 >0成立,若f(cos2θ+2m2+2)<f(sinθ+m2-3m-2)对θ∈R恒成立.
>0成立,若f(cos2θ+2m2+2)<f(sinθ+m2-3m-2)对θ∈R恒成立. )2-
)2- 恒成立,∴m2+3m+4<-
恒成立,∴m2+3m+4<- ,
, )2-
)2- 恒成立,可得3m2-3m-4<-
恒成立,可得3m2-3m-4<- ,
,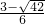 <m<
<m<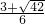 .…
.…

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案