
分析 (1)利用点P(-2,2)在圆O:x2+y2=r2(r>0)上,即可求出r;
(2)利用弦长公式,即可求直线l的方程.
解答 解:(1)∵点P(-2,2)在圆O:x2+y2=r2(r>0)上,
∴r=2$\sqrt{2}$.…(1分)
(2)因为△PAB为等腰三角形,且点P在圆O上,
所以PO⊥AB.
因为PO的斜率$k=\frac{2-0}{-2-0}=-1$,
所以可设直线l的方程为y=x+m.
由$\left\{\begin{array}{l}y=x+m\\{x^2}+{y^2}=8\end{array}\right.$得2x2+2mx+m2-8=0.△=4m2-8×(m2-8)=64-4m2>0,
解得-4<m<4.
设A,B的坐标分别为(x1,y1),(x2,y2),
可得${x_{1,2}}=\frac{{-2m±\sqrt{64-4{m^2}}}}{4}=\frac{{-m±\sqrt{16-{m^2}}}}{2}$.
所以$|AB|=\sqrt{2}|{x_1}-{x_2}|=\sqrt{2(16-{m^2})}=2\sqrt{6}$.
解得m=±2.
所以直线l的方程为x-y+2=0,x-y-2=0.…(5分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
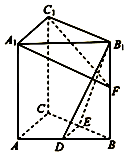 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱BB1上,且B1D⊥A1F,A1C1⊥A1B1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 27 | C. | 28 | D. | 37 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\frac{1}{2}}]$ | B. | [-1,2] | C. | $[{\frac{1}{2},2}]$ | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com