练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设全集I＝R，已知集合M＝{x|(x＋3)2≤0}，N＝{x|x2＋x－6＝0}．

    (1)求(∁IM)∩N；

    (2)记集合A＝(∁IM)∩N，已知集合B＝{x|a－1≤x≤5－a，a∈R}，若B∪A＝A，求实数a的取值范围．


    解：(1)∵M＝{x|(x＋3)2≤0}＝{－3}，

    N＝{x|x2＋x－6＝0}＝{－3,2}，

    ∴∁IM＝{x|x∈R且x≠－3}，

    ∴(∁IM)∩N＝{2}．

    (2)A＝(∁IM)∩N＝{2}，

    ∵A∪B＝A，∴B⊆A，∴B＝Ø或B＝{2}，

    当B＝Ø时，a－1>5－a，∴a>3；

    当B＝{2}时，解得a＝3，

    综上所述，所求a的取值范围为{a|a≥3}．

    [热点预测]


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    以为中点的抛物线的弦所在直线方程为：             ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下面几个命题：

    ①“若x>2，则x>3”的否命题；

    ②“∀a∈(0，＋∞)，函数y＝ax在定义域内单调递增”的否定；

    ③“π是函数y＝sin x的一个周期”或“2π是函数y＝sin 2x的一个周期”；

    ④“x2＋y2＝0”是“xy＝0”的必要条件．

    其中真命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝x2，g(x)＝－m，若对∀x1∈[－1,3]，∃x2∈[0,2], f(x1)≥g(x2)，则实数m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{(0,1)，(1,1)，(－1,2)}，B＝{(x，y)|x＋y－1＝0，x，y∈Z}，则A∩B＝______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(x)对于任意实数x恒有2f(x)－f(－x)＝3x＋1，则f(x)＝(　　)

    A．x－1                                 B．x＋1

    C．2x＋1                                D．3x＋3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b为两个不相等的实数，集合M＝{a2－4a，－1}，N＝{b2－4b＋1，－2}，f：x→x表示把M中的元素x映射到集合N中仍为x，则a＋b等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)的定义域为[0,1]，且同时满足以下三个条件：①f(1)＝1；②对任意的x∈[0,1]，都有f(x)≥0；③当x≥0，y≥0，x＋y≤1时总有f(x＋y)≥f(x)＋f(y)．

    (1)试求f(0)的值；

    (2)求f(x)的最大值；

    (3)证明：当x∈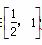时，恒有2x≥f(x)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在淘宝网上，某店铺专卖当地某种特产，由以往的经验表明，不考虑其他因素，该特产每日的销售量y(单位：千克)与销售价格x(单位：元/千克，1<x≤5)满足：当1<x≤3时，y＝a(x－3)2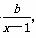＋，(a，b为常数)；当3<x≤5时，y＝－70x＋490，已知当销售价格为2元/千克时，每日可售出该特产700千克；当销售价格为3元/千克时，每日可售出该特产150千克．

    (1)求a，b的值，并确定y关于x的函数解析式；

    (2)若该特产的销售成本为1元/千克，试确定销售价格x的值，使店铺每日销售该特产所获利润f(x)最大(x精确到0.01元/千克)．

    查看答案和解析>>

    同步练习册答案