练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知双曲线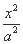-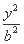=1(a>0,b>0),A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则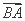与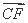夹角的余弦值为　　　　. 



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若直线a与平面α不垂直,那么在平面α内与直线a垂直的直线条数为　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    圆x2-2x+y2-3=0的圆心到直线x+y-3=0的距离为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系中,以坐标原点为极点、x轴的非负半轴为极轴建立坐标系.已知点A的极坐标为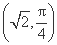,直线l的极坐标方程为ρcos=a,且点A在直线l上.

    (1) 求a的值及直线l的直角坐标方程;

    (2) 圆C的参数方程为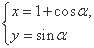(α为参数),试判断直线l与圆C的位置关系.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中,设椭圆与双曲线y2-3x2=3共焦点,且经过点(,2),则该椭圆的离心率为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在(1-x)5+(1-x)6的展开式中,含x3的项的系数是　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合M＝{－1,0,1}，N＝{a，a2}，则使M∪N＝M成立的a的值是(　　)

    A．－1                                 B．0

    C．1                                   D．1或－1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列语句表达中是算法的有(　　)个(　　)

    ①从济南去巴黎可以先乘火车到北京，再乘飞机到巴黎；

    ②利用公式S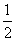＝ah计算底为1，高为2的三角形的面积；

    ③解不等式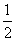x＞2x＋4；

    ④求过点M(1,2)与点N(－3，－5)的直线的方程，可先求直线的斜率，再利用点斜式求得方程．

    A．1　　　                         B．2

    C．3　　　                         D．4

    查看答案和解析>>

    同步练习册答案