
| A. | $(0,\frac{1}{e})$ | B. | (0,e) | C. | $(\frac{1}{e},e)$ | D. | $(\frac{1}{e},+∞)$ |
分析 根据题意,令g(x)=xf(x),分析可得g′(x)=[xf(x)]′=$xf'(x)+f(x)=\frac{lnx}{x}$,对g(x)求积分可得g(x)的解析式,进而可得f(x)的解析式,再令h(x)=f(x)-x,对其求导可得h′(x)=f′(x)-1<0,分析可得函数h(x)=f(x)-x在(0,+∞)上递减,将不等式$f(x)+e>x+\frac{1}{e}$变形可得f(x)-x>$\frac{1}{e}$-e=f(e)-e,结合函数的单调性分析可得答案.
解答 解:根据题意,令g(x)=xf(x),
则有g′(x)=[xf(x)]′=$xf'(x)+f(x)=\frac{lnx}{x}$,
则g(x)=$\frac{1}{2}$(lnx)2+C,即xf(x)=$\frac{1}{2}$(lnx)2+C,
则有f(x)=$\frac{1}{2x}$(lnx)2+$\frac{C}{x}$,
又由$f(e)=\frac{1}{e}$,即f(e)=$\frac{1}{2e}$+$\frac{C}{e}$=$\frac{1}{e}$,解可得C=$\frac{1}{2}$,
故f(x)=$\frac{1}{2x}$(lnx)2+$\frac{1}{2x}$,
令h(x)=f(x)-x,
则h′(x)=f′(x)-1=$\frac{-(lnx+1)^{2}}{2{x}^{2}}-1$<0,
故函数h(x)=f(x)-x在(0,+∞)上递减,
不等式$f(x)+e>x+\frac{1}{e}$,即f(x)-x>$\frac{1}{e}$-e=f(e)-e,
则有0<x<e,
即不等式$f(x)+e>x+\frac{1}{e}$的解集为(0,e);
故选:B.
点评 本题考查抽象函数的单调性,涉及导数的计算以及函数的积分计算,关键是求出函数f(x)的解析式.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数φ(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若把函数φ(x)的图象纵坐标不变,横坐标扩大到原来的2倍,得到函数f(x).
函数φ(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若把函数φ(x)的图象纵坐标不变,横坐标扩大到原来的2倍,得到函数f(x).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
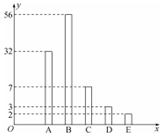 某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{9}{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费次数 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
| 收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
| 消费次数 | 1次 | 2次 | 3次 | 4次 | 5次 |
| 频数 | 60 | 20 | 10 | 5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com