
| A. | 把函数f(x)图象上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移$\frac{π}{4}$个单位长度,可得到函数g(x)的图象 | |
| B. | 两个函数的图象均关于直线$x=-\frac{π}{4}$对称 | |
| C. | 两个函数在区间$(-\frac{π}{4},\frac{π}{4})$上都是单调递增函数 | |
| D. | 函数y=g(x)在[0,2π]上只有4个零点 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象以及性质,得出结论.
解答 解:∵函数f(x)=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),$g(x)=\sqrt{2}sin2x$,
故把f(x)的图象向右平移$\frac{π}{4}$个单位,得到y=$\sqrt{2}$sinx的图象,再把横坐标变为原来的一半,可得g(x)=$\sqrt{2}$sin2x的图象,故A不对.
当x=-$\frac{π}{4}$时,f(x)=0,不是最值,故f(x)的图象不关于直线$x=-\frac{π}{4}$对称,故排除B.
在区间$(-\frac{π}{4},\frac{π}{4})$上,x+$\frac{π}{4}$∈(-$\frac{π}{2}$,$\frac{π}{2}$),2x∈(-$\frac{π}{2}$,$\frac{π}{2}$),故f(x)和g(x)在区间$(-\frac{π}{4},\frac{π}{4})$上都是单调递增函数,故C正确.
在[0,2π]上,2x∈[0,4π],由g(x)=0,可得2x=0,π,2π,3π,4π,即x=0,$\frac{π}{2}$,π,$\frac{3π}{2}$,2π,共计5个零点,故D错误,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象以及性质,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
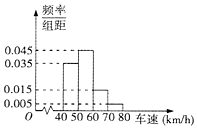 某市交管部门对一路段限速60km/h,为调查违章情况,对经过该路段的300辆汽车进行检测,将所得数据按[40,50),[50.60),[60,70),[70,80)(所有车辆的车速均在[40,80]内)分成四组,绘制成如图所示的频率分布直方图.
某市交管部门对一路段限速60km/h,为调查违章情况,对经过该路段的300辆汽车进行检测,将所得数据按[40,50),[50.60),[60,70),[70,80)(所有车辆的车速均在[40,80]内)分成四组,绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com