练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

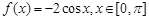    、对于函数与函数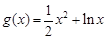有下列命题：

    ①无论函数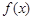的图像通过怎样的平移所得的图像对应的函数都不会是奇函数；

    ②函数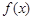的图像与两坐标轴及其直线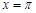所围成的封闭图形的面积为4；

    ③方程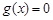有两个根；  

    ④函数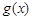图像上存在一点处的切线斜率小于0；

    ⑤若函数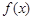在点P处的切线平行于函数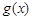在点Q处的切线，则直线PQ的斜率为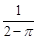，其中正确的命题是________.（把所有正确命题的序号都填上）

     

    【答案】

    ②⑤

    【解析】函数向左平移个单位所得的为奇函数，故①错；

    函数 f（x）的图象与坐标轴及其直线x=π,所围成的封闭图形的面积为2.，故②对；函数的导函数,所以函数g（x）在定义域内为增函数，故③与④错；同时要使函数f（x）在点P处的切线平行于函数g（x），

    在点Q处的切线只有，这时,,所以，⑤正确．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对于函数f（x）=a x2+（b+1）x+b-2（a≠0），若存在实数 x0，使f（ x0）=x0成立，则称 x0为f（x）的不动点
    （1）当a=2，b=-2时，求f（x）的不动点；
    （2）若对于任何实数b，函数f（x）恒有两个相异的不动点，求实数a的取值范围；
    （3）在（2）的条件下判断直线L：y=ax+1与圆（x-2）2+（y+2）2=4 a2+4的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=ax2+kbx（x＞0）与函数g（x）=ax+blnx，a、b、k为常数，它们的导函数分别为y=f′（x）与y=g′（x）
    （1）若g（x）图象上一点p（2，g（2））处的切线方程为：x-2y+2ln2-2=0，求a、b的值；
    （2）对于任意的实数k，且a、b均不为0，证明：当ab＞0时，y=f′（x）与y=g′（x）的图象有公共点；
    （3）在（1）的条件下，设A（x1，y1），B（x2，y2），（x1＜x2）是函数y=g（x）的图象上两点，g′(x0)=
    y2-y1x2-x1
    ，证明：x1＜x0＜x2．

    查看答案和解析>>

    科目：高中数学 来源：河南省卢氏二高2009－2010学年高一上学期期末考试数学试题 题型：044

    对于函数f(x)＝ax2＋(b＋1)x＋b－2(a≠0)，若存在实数x0，使f(x0)＝x0成立，则称x0为f(x)的不动点

    (1)当a＝2，b＝－2时，求f(x)的不动点；

    (2)若对于任何实数b，函数f(x)恒有两个相异的不动点，求实数a的取值范围；

    (3)在(2)的条件下判断直线L：y＝ax＋1与圆(x－2)2＋(y＋2)2＝4a2＋4的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年宣武区质量检一文）定义：如果对于函数定义与内的任意x, 都有（M为常数），那么称M为的下界，下界M中的最大值叫做的下确界。现给出下列函数，其中所有有下确界的函数是                                          （  ）

      ①=cosx   ②  ③   ④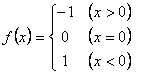

    A. ①        B. ④                 C.②③④              D. ①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于函数与函数有下

    列命题：

    ①函数的图像关于对称；

    ②函数有且只有一个零点；

    ③函数和函数图像上存在平行的切线；

    ④若函数在点P处的切线平行于函数在点Q处的切线，则直线PQ的斜率为

           其中正确的命题是         。（将所有正确命题的序号都填上）

    查看答案和解析>>

    同步练习册答案