【题目】如图，在四棱锥PABCD中，侧面PAB⊥底面ABCD，底面ABCD为矩形，PA＝PB，O为AB的中点，OD⊥PC.

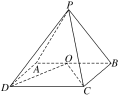
(1)求证：OC⊥PD；

(2)若PD与平面PAB所成的角为30°，求二面角DPCB的余弦值．

参考答案：

【答案】见解析

【解析】解：(1)证明：连接OP，∵PA＝PB，O为AB的中点，

∴OP⊥AB.

∵侧面PAB⊥底面ABCD，

∴OP⊥平面ABCD，

∴OP⊥OD，OP⊥OC.

∵OD⊥PC，OP∩PC＝P，

∴OD⊥平面OPC，

∵OC平面OPC，∴OD⊥OC，

又OP⊥OC，OD∩OP＝O，

∴OC⊥平面OPD，

∵PD平面OPD，∴OC⊥PD.

(2)取CD的中点E，以O为坐标原点，OE，OB，OP所在的直线分别为x轴，y轴，z轴建立空间直角坐标系Oxyz。

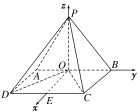
在矩形ABCD中，由(1)得OD⊥OC，

∴AB＝2AD，不妨设AD＝1，则AB＝2。

∵侧面PAB⊥底面ABCD，底面ABCD为矩形，

∴DA⊥平面PAB，CB⊥平面PAB，△DPA≌△CPB，

∴∠DPA为直线PD与平面PAB所成的角，

∴∠DPA＝30°，∠CPB＝30°，PA＝PB＝，

∴B(0，1，0)，C(1，1，0)，D(1，－1，0)，P(0，0，)，从而＝(1，1，－)，＝(0，－2，0)．

设平面PCD的法向量为n1＝(x1，y1，z1)，

得

可取n1＝(，0，1)．

同理，可取平面PCB的一个法向量为n2＝(0，－，－1)．

于是cos〈n1，n2〉＝＝－，

∴二面角DPCB的余弦值为－。

关闭