【题目】某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段： 
， 
， 
，…
后得到如下频率分布直方图.
（1）根据频率分布直方图，估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数；（小数点后保留一位有效数字）
（2）用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本，则各分数段抽取的人数分别是多少？
【答案】（1）71；（2）抽取人数依次为2人；3人；3人；6人；5人；1人
【解析】【试题分析】（1）依据题设提供的频率分布直方图中的图形信息与数据信息可知众数为75，，中位数为70．3，平均数为
。（2）按照分层抽样的思想方法求出各层的抽取的比例为1:3，然后计算出各层的人数分别为6,9,9,18,15,3，进而算出所抽取的人数2人；3人；3人；6人；5人；1人。
解：（1）由图可知众数为75，当分数x<70．3时对应的频率为0．5，所以中位数为70．3，平均数为
（2）各层抽取比例为
，各层人数分别为6,9,9,18,15,3，所以抽取人数依次为2人；3人；3人；6人；5人；1人
科目：高中数学 来源： 题型：
【题目】设P、Q为两个非空集合，定义集合P+Q={m+n| m∈P，n∈Q}，若P={0，2，5}， Q={1，2，6}，则P+Q中元素的个数为 （ ）
A. 9 B. 8 C. 7 D. 6
查看答案和解析>>
科目：高中数学 来源： 题型：
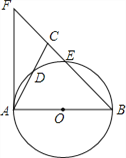
【题目】如图，在△ABC中，BA=BC，以AB为直径的⊙O分别交AC、BC于点D、E，BC的延长线于⊙O的切线AF交于点F．
（1）求证：∠ABC=2∠CAF；
（2）若
，CE∶EB=1∶4，求CE的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中，正确的有( )
①函数y＝
的定义域为{x|x≥1}；
②函数y＝x2＋x＋1在(0，＋∞)上是增函数；
③函数f(x)＝x3＋1(x∈R)，若f(a)＝2，则f(－a)＝－2；
④已知f(x)是R上的增函数，若a＋b>0，则有f(a)＋f(b)>f(－a)＋f(－b)．
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，以原点
为圆心，椭圆
的长半轴长为半径的圆与直线
相切．
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）已知点
，
为动直线
与椭圆
的两个交点，问：在
轴上是否存在定点
，使得
为定值？若存在，试求出点
的坐标和定值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两人练习罚球，每人练习6组，每组罚球20个，命中个数茎叶图如下：
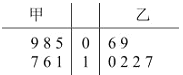
（1）求甲命中个数的中位数和乙命中个数的众数；
（2）通过计算，比较甲乙两人的罚球水平.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
，直线
， 
.
（1）求证：对
，直线
与圆
总有两个不同的交点
；
（2）求弦
的中点
的轨迹方程，并说明其轨迹是什么曲线；
（3）是否存在实数
，使得原
上有四点到直线
的距离为
？若存在，求出
的范围；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥PABCD中，侧面PAB⊥底面ABCD，底面ABCD为矩形，PA＝PB，O为AB的中点，OD⊥PC.
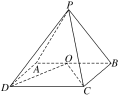
(1)求证：OC⊥PD；
(2)若PD与平面PAB所成的角为30°，求二面角DPCB的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
