
【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线;
的轨迹方程,并说明其轨迹是什么曲线;
(3)是否存在实数![]() ,使得原
,使得原![]() 上有四点到直线
上有四点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
【答案】(1)见解析;(2)M的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆;(3)
为半径的圆;(3)![]() 或
或![]() .
.
【解析】【试题分析】(1)依据题设可以运用圆心与直线的距离或考虑动直线过定点分析判断;(2)借助题设条件运用圆心与弦中点的连线与直线垂直建立方程求解;(3)依据题设借助图形的直观,运用圆心距与直线的位置和数量关系建立不等式:
(1)圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,所以圆心C到直线
,所以圆心C到直线![]() 的距离
的距离 .
.
所以直线![]() 与圆C相交,即直线
与圆C相交,即直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
或:直线![]() 的方程可化为
的方程可化为![]() ,无论m怎么变化,直线
,无论m怎么变化,直线![]() 过定点
过定点![]() ,由于
,由于![]() ,所以点
,所以点![]() 是圆C内一点,故直线
是圆C内一点,故直线![]() 与圆
与圆![]() 总有两个不同的交点.
总有两个不同的交点.
(2)设中点为![]() ,因为直线
,因为直线![]() 恒过定点
恒过定点![]() ,
,
当直线![]() 的斜率存在时,
的斜率存在时, ![]() ,又
,又![]() ,
, ![]() ,
,
所以![]() ,化简得
,化简得![]() .
.
当直线![]() 的斜率不存在时,中点
的斜率不存在时,中点![]() 也满足上述方程.
也满足上述方程.
所以M的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
(3) 假设存在直线![]() ,使得圆上有四点到直线
,使得圆上有四点到直线![]() 的距离为
的距离为![]() ,由于圆心
,由于圆心![]() ,半径为
,半径为![]() ,则圆心
,则圆心![]() 到直线
到直线![]() 的距离为
的距离为
化简得![]() ,解得
,解得![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,已知底角为45的等腰梯形ABCD,底边BC长为7cm,腰长为![]() ,当一条垂直于底边BC
,当一条垂直于底边BC
(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x
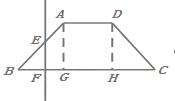
(1)试写出直线l左边部分的面积f(x)与x的函数.
(2)已知A={x|f(x)<4},B={x|a2<x<a+2},若A∪B=B,求a的取值范围。.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: ![]() ,
, ![]() ,
, ![]() ,…
,…![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.

(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(2)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2-xlna,a>1.
(1)求证:函数f(x)在(0,+∞)上单调递增;
(2)对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是R上的偶函数,且当x>0时,函数的解析式为f(x)=![]() .
.
(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求当x<0时,函数的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新一届班委会的7名成员有![]() 、
、![]() 、
、![]() 三人是上一届的成员,现对7名成员进行如下分工.
三人是上一届的成员,现对7名成员进行如下分工.
(Ⅰ)若正、副班长两职只能由![]() 、
、![]() 、
、![]() 三人选两人担任,则有多少种分工方案?
三人选两人担任,则有多少种分工方案?
(Ⅱ)若![]() 、
、![]() 、
、![]() 三人不能再担任上一届各自的职务,则有多少种分工方案?
三人不能再担任上一届各自的职务,则有多少种分工方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com