
【题目】已知函数f(x)=ax+x2-xlna,a>1.
(1)求证:函数f(x)在(0,+∞)上单调递增;
(2)对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范围.
【答案】(1)见解析(2)1<a≤e.
【解析】试题分析:(1)根据函数的解析式,得到![]() ,由
,由![]() ,且
,且![]() 时,得到
时,得到![]() ,即可证得函数在
,即可证得函数在![]() 单调递增;
单调递增;
(2)由(1)得到函数的单调性,求解函数的最值,令![]() ,可得
,可得![]() 为单调递增函数,得
为单调递增函数,得![]() ,即可得到函数的最值,即可作出证明.
,即可得到函数的最值,即可作出证明.
试题解析: (1)证明:f′(x)=axlna+2x-lna=2x+(ax-1)lna,
由于a>1,故当x∈(0,+∞)时,lna>0,ax-1>0,所以f′(x)>0,
故函数f(x)在(0,+∞)上单调递增.
(2)由(1)可知,当x∈(-∞,0)时,f′(x)<0,
故函数f(x)在(-∞,0)上单调递减.
所以,f(x)在区间[-1,0]上单调递减,在区间[0,1]上单调递增.
所以f(x)min=f(0)=1, f(x)max=max{f(-1),f(1)},
f(-1)=![]() +1+lna,f(1)=a+1-lna,
+1+lna,f(1)=a+1-lna,
f(1)-f(-1)=a-![]() -2lna,
-2lna,
记g(x)=x-![]() -2lnx,g′(x)=1+
-2lnx,g′(x)=1+![]() -
-![]() =
=![]() 2≥0,
2≥0,
所以g(x)=x-![]() -2lnx递增,故f(1)-f(-1)=a-
-2lnx递增,故f(1)-f(-1)=a-![]() -2lna>0,
-2lna>0,
所以f(1)>f(-1),于是f(x)max=f(1)=a+1-lna,
故对任意x1,x2∈[-1,1],|f(x1)-f(x2)|max=|f(1)-f(0)|=a-lna,
a-lna≤e-1,所以1<a≤e.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() :
: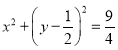 经过椭圆
经过椭圆![]() :
:![]() (
(![]() )的左右焦点
)的左右焦点![]() ,
,![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
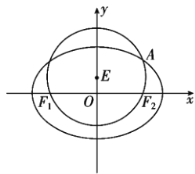
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设与直线![]() (
(![]() 为原点)平行的直线
为原点)平行的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.当
两点.当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①函数y=![]() 的定义域为{x|x≥1};
的定义域为{x|x≥1};
②函数y=x2+x+1在(0,+∞)上是增函数;
③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2;
④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数茎叶图如下:
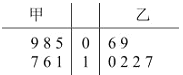
(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线;
的轨迹方程,并说明其轨迹是什么曲线;
(3)是否存在实数![]() ,使得原
,使得原![]() 上有四点到直线
上有四点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
⑵若![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根![]() 的取值范围;
的取值范围;
⑶若![]() ,
,![]() ,求使
,求使![]() 得图像恒在
得图像恒在![]() 图像上方的最大正整数
图像上方的最大正整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ﹥
﹥![]() ﹥0)的离心率为
﹥0)的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为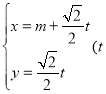 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .且曲线
.且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com