
【题目】某商店为了吸引顾客,设计了一个摸球小游戏,顾客从装有1个红球,1个白球,3个黑球的袋中一次随机的摸2个球,设计奖励方式如下表:
结果 | 奖励 |
1红1白 | 10元 |
1红1黑 | 5元 |
2黑 | 2元 |
1白1黑 | 不获奖 |
(1)某顾客在一次摸球中获得奖励X元,求X的概率分布表与数学期望;
(2)某顾客参与两次摸球,求他能中奖的概率.
【答案】(1)概率分布表为:
X | 10 | 5 | 2 | 0 |
P |
|
|
|
|
E(X)=3.1元.
(2)![]() .
.
【解析】
试题分析:(1)因为P(X=10)=![]() =
=![]() ,P(X=5)=
,P(X=5)=![]() =
=![]() ,P(X=2)=
,P(X=2)=![]() =
=![]() ,P(X=0) =
,P(X=0) =![]() =
=![]() ,
,
所以X的概率分布表为:
X | 10 | 5 | 2 | 0 |
P |
|
|
|
|
从而E(X)=10![]() +5
+5![]() +2
+2![]() +0
+0![]() =3.1元.
=3.1元.
(2)能中奖指至少有一次中奖,因为一次中奖的概率为![]() ,所以一次不中奖的概率为
,所以一次不中奖的概率为![]() ,两次皆不中奖概率为
,两次皆不中奖概率为![]()
![]() ,因此至少有一次中奖概率为1-
,因此至少有一次中奖概率为1-![]()
![]() =
=![]() .
.
试题解析:解:(1)因为P(X=10)=![]() =
=![]() ,P(X=5)=
,P(X=5)=![]() =
=![]() ,
,
P(X=2)=![]() =
=![]() ,P(X=0) =
,P(X=0) =![]() =
=![]() ,
,
所以X的概率分布表为:
X | 10 | 5 | 2 | 0 |
P |
|
|
|
|
从而E(X)=10![]() +5
+5![]() +2
+2![]() +0
+0![]() =3.1元. 6分
=3.1元. 6分
(2)记该顾客一次摸球中奖为事件A,由(1)知,P(A)=![]() ,
,
从而他两次摸球中至少有一次中奖的概率P=1-[1-P(A)]2=![]() .
.
答:他两次摸球中至少有一次中奖的概率为![]() . 10分.
. 10分.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.
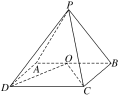
(1)求证:OC⊥PD;
(2)若PD与平面PAB所成的角为30°,求二面角DPCB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吉安一中举行了一次“环保知识竞赛”活动,为了解本了次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照 ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛学生成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的
名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的![]() 名同学中得分在
名同学中得分在![]() 的学生人数恰有一人的概率.
的学生人数恰有一人的概率.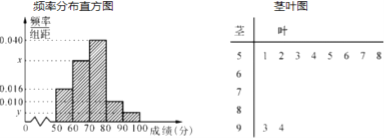
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
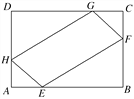
(1)写出四边形EFGH的面积y与x之间的函数关系;
(2)求当x为何值时y取得最大值,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),现以原点为极点,
为参数),现以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上是否存在一点
上是否存在一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最小?若存在,求出距离的最小值及点
的距离最小?若存在,求出距离的最小值及点![]() 的直角坐标;若不存在,请说明理由.
的直角坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
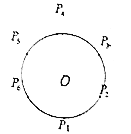
【题目】如图,设![]() 为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量
为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量![]() .
.
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年5月,我省南昌市遭受连日大暴雨天气,某网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票,按照南昌暴雨前后两个时间收集有效投票,暴雨后的投票收集了![]() 份,暴雨前的投票也收集了
份,暴雨前的投票也收集了![]() 份,所得统计结果如下表:
份,所得统计结果如下表:

已知工作人与从所有投票中任取一个,取到“不支持投入”的投票的概率为![]() .
.
(1)求列表中数据的值;
(2)能够有多大的把握认为南昌暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关系?
附: 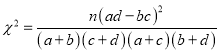
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com