
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上为单调递减函数,求
上为单调递减函数,求![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]()
【解析】
(1)将![]() 代入函数
代入函数![]() 解析式,再求得导函数
解析式,再求得导函数![]() ,并令
,并令![]() 求得极值点,即可确定
求得极值点,即可确定![]() 的符号,确定单调区间.
的符号,确定单调区间.
(2)先求得导函数,由函数![]() 在区间
在区间![]() 上为单调递减函数,可得
上为单调递减函数,可得![]() 在区间
在区间![]() 上恒成立,即
上恒成立,即![]() .构造函数
.构造函数![]() ,即可由函数单调性求得
,即可由函数单调性求得![]() ,解不等式即可求得
,解不等式即可求得![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,其定义域为
,其定义域为![]() ,
,
则![]()
![]() ,
,
令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,故函数
,故函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,故函数
,故函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
所以![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题意得![]() ,
,
因为函数![]() 在区间
在区间![]() 上为单调递减函数,
上为单调递减函数,
所以在区间![]() 上
上![]() 恒成立,
恒成立,
即![]() 在
在![]() 时恒成立,
时恒成立,
即![]() ,
,
即![]() ,其中
,其中![]() ,
,
令![]() ,
,
易知函数![]() 在
在![]() 上单调递增,故
上单调递增,故![]() .
.
所以![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ;
;
故![]() 的取值范围为
的取值范围为![]() .
.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
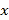
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式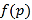 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2018年1月至12月石油进口量统计图(其中同比是今年第![]() 个月与去年第
个月与去年第![]() 个月之比),则下列说法错误的是( )
个月之比),则下列说法错误的是( )
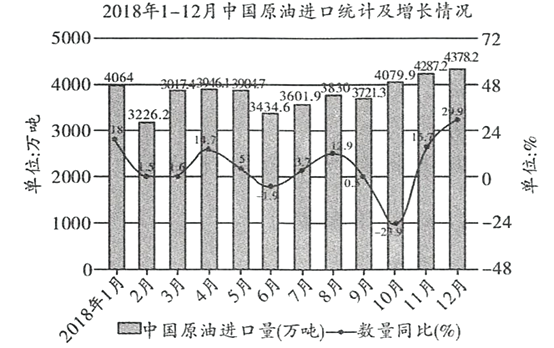
A.2018年下半年我国原油进口总量高于2018年上半年
B.2018年12个月中我国原油月最高进口量比月最低进口量高1152万吨
C.2018年我国原油进口总量高于2017年我国原油进口总量
D.2018年1月—5月各月与2017年同期相比较,我国原油进口量有增有减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,经过点
,经过点![]() 的直线与抛物线
的直线与抛物线![]() 交于不同的
交于不同的![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,经过点
,经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求抛物线![]() 的方程和焦点
的方程和焦点![]() 的坐标;
的坐标;
(2)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中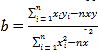 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
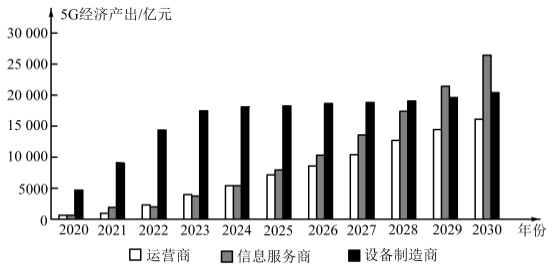
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn+1﹣bn=![]() (n∈N+)且b1=3,求数列
(n∈N+)且b1=3,求数列![]() 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)上一点P![]() 到准线的距离与到原点O的距离相等,抛物线的焦点为F.
到准线的距离与到原点O的距离相等,抛物线的焦点为F.
(1)求抛物线的方程;
(2)若A为抛物线上一点(异于原点O),点A处的切线交x轴于点B,过A作准线的垂线,垂足为点E,试判断四边形AEBF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com