
分析 根据条件a2=-4,S8=a8,可解得等差数列的首项和公差,故an=2n-8,Sn=n(n-7).由an≤0解得n≤4,即数列{an}前3项为负数,第4项为0,从第5项开始为正数.对n分类讨论再利用等差数列的前n项和公式即可得Tn.
解答 解:设等差数列{an}的公差为d,
由S8=a8得8a1+$\frac{8×(8-1)}{2}$d=a1+7d,则a1=-3d.
又a2=a1+d=-4,∴d=2,a1=-6.
∴an=-6+(n-1)×2=2n-8,Sn=$\frac{n({a}_{1}+{a}_{n})}{2}$=$\frac{n[-6+2(n-4)]}{2}$=n(n-7).
由an≤0解得n≤4,即数列{an}前3项为负数,第4项为0,从第5项开始为正数.
∴当n≤4时,Tn=-Sn=n(7-n)=-n2+7n,
当n≥5时,Tn=Sn-S4+(-S4)=Sn-2S4=n(n-7)-2×4×(4-7)=n2-7n+24
∴Tn=$\left\{\begin{array}{l}{-{n}^{2}+7n,n≤4}\\{{n}^{2}-7n+14,n≥5}\end{array}\right.$
点评 本题考查了等差数列的通项公式及其前n项和公式、绝对值数列,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
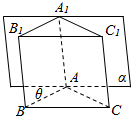 已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的最大值是( )
已知在直三棱柱ABC-A1B1C1中,∠BAC=120°,AB=AC=1,AA1=2,若棱AA1在正视图的投影面α内,且AB与投影面α所成角为θ(30°≤θ≤60°),设正视图的面积为m,侧视图的面积为n,当θ变化时,mn的最大值是( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com