Question

13．如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，∠BAD=60°，侧棱PA⊥底面ABCD，E、F分别是PA、PC的中点．
（Ⅰ）证明：PA∥平面FBD；
（Ⅱ）若PA=1，在棱PC上是否存在一点M使得二面角E-BD-M的大小为60°．若存在，求出PM的长，不存在请说明理由．

Answer 1

分析 （Ⅰ）连接AC交BD于点O，连接OF，推导出FO∥PA，由此能证明PA∥平面FBD．
（Ⅱ） 法一：（先猜后证）点M为PC的中点，即为点F，连接EO，AC⊥BD，BD⊥EO，BD⊥FO，从而∠EOF就是二面角E-BD-F的平面角，由此能求出PM=1．法二：（向量方法探索）以O为坐标原点，如图所示，分别以射线OA，OB，OF为x，y，z轴的正半轴，建立空间直角坐标系O-xyz，利用向量法能求出结果．

解答 证明：（Ⅰ）连接AC交BD于点O，连接OF，
∵O、F分别是AC、PC的中点，
∴FO∥PA…（5分）
∵PA不在平面FBD内，
∴PA∥平面FBD…（6分）
解：（Ⅱ） 解法一：（先猜后证）点M为PC的中点，即为点F，…（8分）
连接EO，∵PA⊥平面ABCD，
∴PA⊥AC，又∵ABCD是菱形，∴AC⊥BD，
∴BD⊥平面PAC，则BD⊥EO，BD⊥FO，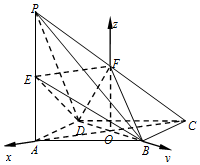
∴∠EOF就是二面角E-BD-F的平面角．…（11分）
连接EF，则EF∥AC，∴EF⊥FO，
∵EF=$\frac{1}{2}AC$=$\frac{\sqrt{3}}{2}$，
在Rt△OFE中，tan∠EOF=$\frac{EF}{OF}$=$\sqrt{3}$，
故$∠EOF=\frac{π}{3}$，∴PM=1．…（15分）
解法二：（向量方法探索）
以O为坐标原点，如图所示，分别以射线OA，OB，OF为x，y，z轴的正半轴，
建立空间直角坐标系O-xyz，由题意可知各点坐标如下：
O（0，0，0），A（$\frac{\sqrt{3}}{2}$，0，0），B（0，$\frac{1}{2}$，0），D（0，$\frac{1}{2}$，0），P（$\frac{\sqrt{3}}{2}$，0，1），E（$\frac{\sqrt{3}}{2}$，0，$\frac{1}{2}$），…（8分）
设平面EBD的法向量为$\overrightarrow{m}$=（x，y，z），
∵$\overrightarrow{DB}$=（0，1，0），$\overrightarrow{DE}$=（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}，\frac{1}{2}$），
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=y=0}\\{\overrightarrow{m}•\overrightarrow{AE}=\frac{\sqrt{3}}{2}x+\frac{1}{2}y+\frac{1}{2}z=0}\end{array}\right.$，取x=1，得$\overrightarrow{m}$=（1，0，-$\sqrt{3}$），…（9分）
设平面BDM的法向量为$\overrightarrow{n}$=（a，b，c），点M（x₀，y₀，z₀），
则由$\overrightarrow{PM}=λ\overrightarrow{PC}$，得M（$\frac{\sqrt{3}}{2}$-$\sqrt{3}λ$，0，1-λ），
∴$\overrightarrow{DM}$=（$\frac{\sqrt{3}}{2}-\sqrt{3}λ，\frac{1}{2}，1-λ$），$\overrightarrow{BM}$=（$\frac{\sqrt{3}}{2}-\sqrt{3}λ$，-$\frac{1}{2}$，1-λ），
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DM}=（\frac{\sqrt{3}}{2}-\sqrt{3}λ）a+\frac{1}{2}b+（1-λ）c=0}\\{\overrightarrow{n}•\overrightarrow{BM}=（\frac{\sqrt{3}}{2}-\sqrt{3}λ）a-\frac{1}{2}b+（1-λ）c=0}\end{array}\right.$，取a=1，解得$\overrightarrow{n}$=（1，0，$\frac{\sqrt{3}λ-\frac{\sqrt{3}}{2}}{1-λ}$），…（13分）
由已知可得cos60°=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{|1-\frac{3λ-\frac{3}{2}}{1-λ}|}{2\sqrt{1+（\frac{\sqrt{3}λ-\frac{\sqrt{3}}{2}}{1-λ}）^{2}}}$，解得$λ=\frac{1}{2}$或$λ=\frac{3}{4}$（舍），
∴点M为棱PC的中点．∴PM=1．…（15分）

点评 本题考查线面平行的证明，考查线段长的求法，是中档题，注意空间思维能力的培养．