
【题目】函数![]() (
(![]() 为实数).
为实数).
(1)若![]() ,求证:函数
,求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(2)求函数![]() 在
在![]() 上的最小值及相应的
上的最小值及相应的![]() 的值;
的值;
(3)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 在
在![]() 上是增函数;(2)见解析;(3)
上是增函数;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)当![]() 时,
时, ![]() 在(0,+∞)上恒成立,故函数在(1,+∞)上是增函数;
在(0,+∞)上恒成立,故函数在(1,+∞)上是增函数;
(2)求导) ![]() ,当x∈[1,e]时,
,当x∈[1,e]时, ![]() .分①
.分①![]() ,②
,②![]() ,③
,③![]() ,三种情况得到函数f(x)在[1,e]上是单调性,进而得到[f(x)]min;
,三种情况得到函数f(x)在[1,e]上是单调性,进而得到[f(x)]min;
(3)由题意可化简得到![]() ,令
,令![]() ,利用导数判断其单调性求出最小值为
,利用导数判断其单调性求出最小值为![]() .
.
试题解析:
(1)当![]() 时,
时, ![]() ,其定义域为
,其定义域为![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立,
故函数![]() 在
在![]() 上是增函数.
上是增函数.
(2) ![]() ,
,
当![]() 时,
时, ![]() ,
,
①若![]() ,
, ![]() 在
在![]() 上有
上有![]() (仅当
(仅当![]() ,
, ![]() 时,
时, ![]() ),
),
故函数![]() 在
在![]() 上是增函数,此时
上是增函数,此时![]() ;
;
②若![]() ,由
,由![]() ,得
,得![]() ,
,
当![]() 时,有
时,有![]() ,此时
,此时![]() 在区间
在区间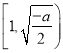 上是减函数;
上是减函数;
当![]() 时,有
时,有![]() ,此时,
,此时, ![]() 在区间
在区间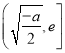 上是增函数,
上是增函数,
故 ;
;
③若![]() ,
, ![]() 在
在![]() 上有
上有![]() (仅当
(仅当![]() ,
, ![]() 时,
时, ![]() ),
),
故函数![]() 在
在![]() 上是减函数,此时
上是减函数,此时![]()
综上可知,当![]() 时,
时, ![]() 的最小值为1,相应的
的最小值为1,相应的![]() 的值为1;
的值为1;
当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,相应的
,相应的![]() 值为
值为![]() ;
;
当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,相应的
,相应的![]() 的值为
的值为![]() .
.
(3)不等式![]() 可化为
可化为![]() ,
,
因为![]() ,所以
,所以![]() ,且等号不能同时取,
,且等号不能同时取,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
令![]() ,
,
则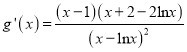 ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
从而![]() (仅当
(仅当![]() 时取等号),
时取等号),
所以![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() 的最小值为
的最小值为![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某品牌手机销售商今年1,2,3月份的销售量分别是1万部,1.2万部,1.3万部,为估计以后每个月的销售量,以这三个月的销售为依据,用一个函数模拟该品牌手机的销售量y(单位:万部)与月份x之间的关系,现从二次函数![]() 或函数
或函数![]() 中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
, ![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 若椭圆![]() 的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,求椭圆
上,求椭圆![]() 的方程;
的方程;
(2)当![]() 时,若点
时,若点![]() 平分线段
平分线段![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处.
海里处.
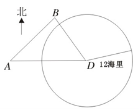
(1)求此时该外国船只与![]() 岛的距离;
岛的距离;
(2)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行,为了将该船拦截在离
海里的速度沿正南方向航行,为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() 是
是![]() 的必要而不充分条件;
的必要而不充分条件;
设命题![]() 实数
实数![]() 满足方程
满足方程![]() 表示双曲线.
表示双曲线.
(1)若“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com