
 的圆心为M,圆(x-2)2+y2=
的圆心为M,圆(x-2)2+y2= 的圆心为N,一动圆与这两圆都外切.
的圆心为N,一动圆与这两圆都外切. 的取值范围.
的取值范围.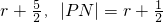 ,
,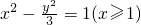

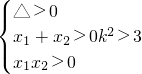 ,
,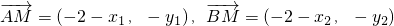 ,
,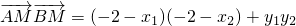 =4+2(x1+x2)+x1x2+k2(x1-2)(x2-2)=
=4+2(x1+x2)+x1x2+k2(x1-2)(x2-2)=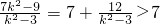
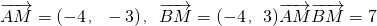 ,
,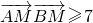
 用k表示,求出k的范围.
用k表示,求出k的范围.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2008年广东地区数学科全国各地模拟试题直线与圆锥曲线大题集 题型:044
已知圆![]() 的圆心为M,圆
的圆心为M,圆![]() 的圆心为N,一动圆与这两圆都外切.
的圆心为N,一动圆与这两圆都外切.
(Ⅰ)求动圆圆心P的轨迹方程.
(Ⅱ)若过点N的直线l与(Ⅰ)中所求轨迹有两个交点A、B,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:辽宁省沈阳二中2008-2009学年高三上学期期中考试(数学理) 题型:044
已知圆![]() 的圆心为M,圆
的圆心为M,圆![]() 的圆心为N,一动圆与这两圆都外切.
的圆心为N,一动圆与这两圆都外切.
(1)求动圆圆心P的轨迹方程;
(2)若过点N的直线l与(1)中所求轨迹有两个交点A、B,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年云南省高一上学期期末考试数学试卷 题型:填空题
已知圆的圆心为M(2,-3),半径为4,则圆M的方程为________________________.
查看答案和解析>>
科目:高中数学 来源:2007-2008学年四川省成都十八中高二(上)期末数学试卷(解析版) 题型:解答题
 的圆心为M,圆(x-2)2+y2=
的圆心为M,圆(x-2)2+y2= 的圆心为N,一动圆与这两圆都外切.
的圆心为N,一动圆与这两圆都外切. 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com