
((12分)已知抛物线C:y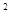 =4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。
=4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。
(1)求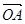 ·
·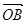 的值;(2)设
的值;(2)设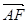 =
=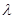
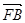 ,求△ABO的面积S的最小值;
,求△ABO的面积S的最小值;
(3)在(2)的条件下若S≤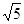 ,求
,求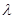 的取值范围。
的取值范围。
⑴根据抛物线的方程可得焦点F(1,0),设直线l的方程为x=my+1,将其与C的方程联立,消去x可得 -4my-4=0.
-4my-4=0.
设A、B点的坐标分别为( ,
, ),(
),( ,
, )(
)( ﹥0﹥
﹥0﹥ ),则
),则
 =-4.
=-4.
因为
 =4
=4 ,
,
 =4
=4 ,所以
,所以
 =
=



 =1,
=1,
故 ·
· =
=
 +
+
 =-3 ………………………………………………4分
=-3 ………………………………………………4分
 (2)因为
(2)因为 =
=
 ,所以(1-
,所以(1- ,-
,- )=
)= (
( -1,
-1, )即 1-
)即 1- =
=
 -
- ①
①
- =
=
 ②
②
又
 =4
=4 ③
③ 
 =4
=4 ④ ,由②③④消去
④ ,由②③④消去 ,
, 后,得到
后,得到 =
=

 ,将其代入①,注意到
,将其代入①,注意到 ﹥0,解得
﹥0,解得 =
= 。
。
从而可得 =-
=- ,
, =2
=2 ,故△OAB的面积S=
,故△OAB的面积S=
 ·
· =
=
因为 ≧2恒成立,故△OAB的面积S的最小值是2………(8分).(3)由
≧2恒成立,故△OAB的面积S的最小值是2………(8分).(3)由  ≦
≦ 解之的
解之的 ≦
≦ ≦
≦ ………………………………………………12分
………………………………………………12分
【解析】略


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com