
分析 若A∩B={1},则11-a=1,或a=1,或2a=1,或lga=1,分类讨论是否存在满足条件的a值,最后综合讨论结果,可得答案.
解答 解:∵集合A={0,1}.B={11-a,a,2a,lga}.
若A∩B={1},
则11-a=1,或a=1,或2a=1,或lga=1,
①当11-a=1时,a=10,
此时lga=1,由集合元素的互异性,可得不满足条件;
②当a=1时,B={10,1,2,0}.
此时,A∩B={0,1}不满足条件;
③2a=1时,a=0,lga无意义不满足条件;
④lga=1时,由①得不满足条件,
综上不存在满足条件的a值.
点评 本题考查的知识点是集合的交集运算,分类讨论思想,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 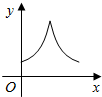 | B. | 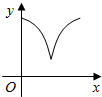 | C. | 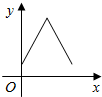 | D. | 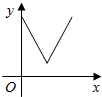 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 200 | 300 | 400 | 500 |
| P | 0.20 | 0.35 | 0.30 | 0.15 |
| A. | 706元 | B. | 690元 | C. | 754元 | D. | 720元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com