
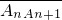 =
=
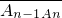 (n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|
(n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|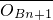 |=|
|=|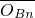 |+2
|+2 (n∈N*),其中B1(3,3).
(n∈N*),其中B1(3,3). kn的值;
kn的值;
 为公比的等比数列
为公比的等比数列
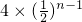 =9-24-n
=9-24-n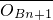 |=|
|=|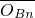 |+2
|+2 (n∈N*),
(n∈N*), xn+1=
xn+1=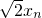 +2
+2
 ,∴
,∴ kn=
kn= =1;
=1; (9-23-n)(2n+3)-
(9-23-n)(2n+3)- =
=
 ,则an+1=
,则an+1=
 ]-[
]-[ ]=
]=
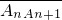 =
=
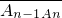 ,可得
,可得 ,从而可得{xn-xn-1}是以4为首项,
,从而可得{xn-xn-1}是以4为首项, 为公比的等比数列;利用射线y=x(x≥0)上,满足|
为公比的等比数列;利用射线y=x(x≥0)上,满足|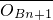 |=|
|=|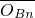 |+2
|+2 (n∈N*),可得{xn}是以3为首项,2为公差的等差数列,由此可用n表示点An与Bn的坐标;
(n∈N*),可得{xn}是以3为首项,2为公差的等差数列,由此可用n表示点An与Bn的坐标; ,从而可求
,从而可求 kn的值;
kn的值; (9-23-n)(2n+3)-
(9-23-n)(2n+3)- =
= ,确定函数的单调性,从而可求四边形AnAn+1Bn+1Bn面积S的取值范围.
,确定函数的单调性,从而可求四边形AnAn+1Bn+1Bn面积S的取值范围.

科目:高中数学 来源: 题型:
| x | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| AnAn+1 |
| 1 |
| 2 |
. |
| An-1An |
. |
| OBn+1 |
. |
| OBn |
| 2 |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源:2012年上海市静安、杨浦、青浦、宝山区高考数学二模试卷(文科)(解析版) 题型:解答题
 =
=
 (n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|
(n≥2,n∈N*),其中A1(1,0),A2(5,0);点B1,B2,…Bn,…在射线y=x(x≥0)上,满足|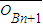 |=|
|=|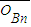 |+2
|+2 (n∈N*),其中B1(3,3).
(n∈N*),其中B1(3,3).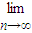 kn的值;
kn的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com