
现有A,B两球队进行友谊比赛,设A队在每局比赛中获胜的概率都是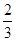 .
.
(Ⅰ)若比赛6局,求A队至多获胜4局的概率;
(Ⅱ)若采用“五局三胜”制,求比赛局数ξ的分布列和数学期望.
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:解答题
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.
(Ⅰ)写出数量积X的所有可能取值;
(Ⅱ)分别求小波去下棋的概率和不去唱歌的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业招聘工作人员,设置 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加 组测试,丙、丁两人各自独立参加
组测试,丙、丁两人各自独立参加 组测试.已知甲、乙两人各自通过测试的概率均为
组测试.已知甲、乙两人各自通过测试的概率均为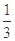 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加 组测试,
组测试, 组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功.
组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功.
(Ⅰ)求戊竞聘成功的概率;
(Ⅱ)求参加 组测试通过的人数多于参加
组测试通过的人数多于参加 组测试通过的人数的概率;
组测试通过的人数的概率;
(Ⅲ)记 、
、 组测试通过的总人数为
组测试通过的总人数为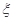 ,求
,求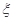 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
(Ⅰ)求乙得分的分布列和数学期望;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
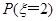 ;
;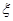 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | 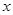 |
| B | 12 | 3 |
| C | 8 | 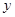 |
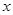 与
与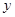 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学参加省学业水平测试,物理、化学、生物获得等级 和获得等级不是
和获得等级不是 的机会相等,物理、化学、生物获得等级
的机会相等,物理、化学、生物获得等级 的事件分别记为
的事件分别记为 、
、 、
、 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是 的事件分别记为
的事件分别记为 、
、 、
、 .
.
(Ⅰ)试列举该同学这次水平测试中物理、化学、生物成绩是否为 的所有可能结果(如三科成绩均为
的所有可能结果(如三科成绩均为 记为
记为 );
);
(Ⅱ)求该同学参加这次水平测试获得两个 的概率;
的概率;
(Ⅲ)试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件,使该事件的概率大于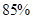 ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同,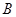 箱中没有球.我们把从
箱中没有球.我们把从 箱中取1个球放入
箱中取1个球放入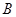 箱中,然后在
箱中,然后在 箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
(1)分别求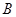 箱中恰有1个、2个、3个白球的概率;
箱中恰有1个、2个、3个白球的概率;
(2)从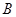 箱中一次取出2个球,记白球的个数为
箱中一次取出2个球,记白球的个数为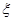 ,求
,求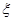 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com