
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
(Ⅰ)求乙得分的分布列和数学期望;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
(Ⅰ)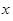 的分布列为
的分布列为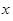
0 15 30 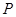
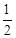

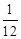
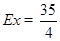 ;(Ⅱ)甲、乙两人中至少有一人入选的概率
;(Ⅱ)甲、乙两人中至少有一人入选的概率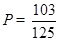 .
.
解析试题分析:(Ⅰ)此题属于答错扣分问题,得分最低为零分,它包括两种情况,一种是三个都答错,一种是三个答对一个,若三个答对两个,此时得分为15分,若三个答对三个,此时得分为30分,故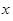 =
=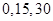 ,计算出各个概率,可得分布列,从而求出数学期望;(Ⅱ)甲、乙两人中至少有一人入选,像这种至少有一问题,常常采用对立事件来解,即甲乙都没入选,分别求出甲乙没入选的概率,从而求出甲、乙两人中至少有一人入选的概率.
,计算出各个概率,可得分布列,从而求出数学期望;(Ⅱ)甲、乙两人中至少有一人入选,像这种至少有一问题,常常采用对立事件来解,即甲乙都没入选,分别求出甲乙没入选的概率,从而求出甲、乙两人中至少有一人入选的概率.
试题解析:(Ⅰ)设乙得分为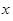 ,则
,则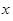 =
=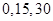 ,
,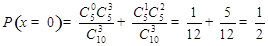 ,
,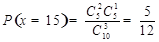 ,
,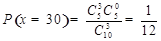
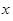 的分布列为
的分布列为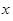
0 15 30 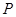
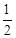

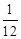
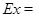
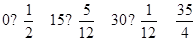 ;
;
(Ⅱ)设“甲入选”为事件A,“乙入选”为事件B,则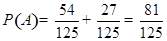 ,
, ,
,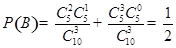 ,
,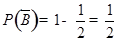 ,所求概率
,所求概率
考点:本小题考查独立事件与对立事件的概率,分布列,数学期望,考查学生的分析问题、解决问题的能力.


科目:高中数学 来源: 题型:解答题
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是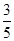 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是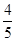 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用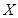 表示张同学答对题的个数,求
表示张同学答对题的个数,求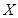 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某校高一年级学生参加社区服务次数统计,随机抽取了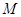 名学生作为样本,得到这
名学生作为样本,得到这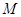 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下: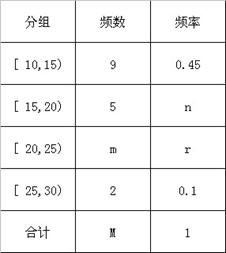
(1)求出表中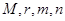 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于 次的学生中任选
次的学生中任选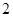 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中有红球3个,白球4个.
(Ⅰ)从中不放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,求摸2次恰好第2次中奖的概率;
(Ⅱ)每次同时摸2个,并放回,摸到的2个球中至少有1个红球则中奖,连续摸4次,求中奖次数X的数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小明参加完高考后,某日路过一家电子游戏室,注意到一台电子游戏机的规则是:你可在1,2,3,4,5,6点中选一个,押上赌注a元。掷3枚骰子,如果所押的点数出现1次、2次、3次,那么原来的赌注仍还给你,并且你还分别可以收到赌注的1倍、2倍、3倍的奖励。如果所押的点数不出现,那么赌注就被庄家没收。
(1)求掷3枚骰子,至少出现1枚为1点的概率;
(2)如果小明准备尝试一次,请你计算一下他获利的期望值,并给小明一个正确的建议。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有A,B两球队进行友谊比赛,设A队在每局比赛中获胜的概率都是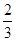 .
.
(Ⅰ)若比赛6局,求A队至多获胜4局的概率;
(Ⅱ)若采用“五局三胜”制,求比赛局数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋子里装有7个球, 其中有红球4个, 编号分别为1,2,3,4; 白球3个, 编号分别为2,3,4. 从袋子中任取4个球 (假设取到任何一个球的可能性相同).
(Ⅰ) 求取出的4个球中, 含有编号为3的球的概率;
(Ⅱ) 在取出的4个球中, 红球编号的最大值设为X ,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某社团组织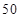 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| | 宣传慰问 | 义工 | 总计 |
| 20至40岁 | 11 | 16 | 27 |
| 大于40岁 | 15 | 8 | 23 |
| 总计 | 26 | 24 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com