

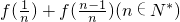 的值;
的值;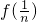 +
+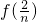 +…+
+…+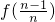 +f(1)(n∈N*),求数列{an}的通项公式;
+f(1)(n∈N*),求数列{an}的通项公式; +
+ =
= +
+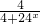 =1
=1 )+f(
)+f( )=1.(5分)
)=1.(5分)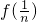 +
+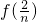 +…+
+…+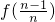 +f(1)(n∈N*),①
+f(1)(n∈N*),①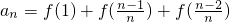 +…+f(
+…+f( )+f(0)(n∈N*),②
)+f(0)(n∈N*),② )+f(
)+f( )=1,
)=1,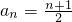 .(10分)
.(10分) ,∴
,∴ ,
,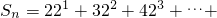 (n+1)•2n,①
(n+1)•2n,① ,
, ,且 g(1)=k-2-2>0,而函数f(x)在[1,+∞) 是增函数,
,且 g(1)=k-2-2>0,而函数f(x)在[1,+∞) 是增函数, +
+ =
= +
+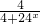 =1,能得到f(
=1,能得到f( )+f(
)+f( )=1.由此规律求值即可
)=1.由此规律求值即可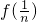 +
+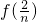 +…+
+…+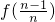 +f(1)(n∈N*),知
+f(1)(n∈N*),知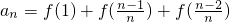 +…+f(
+…+f( )+f(0)(n∈N*),由倒序相加法能得到
)+f(0)(n∈N*),由倒序相加法能得到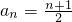 .
. ,知
,知 ,由
,由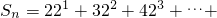 (n+1)•2n,利用错位相减法能求出Sn=n•2n+1,要使得不等式knSn>4bn恒成立,即kn2-2n-2>0对于一切的n∈N*恒成立,由此能够证明当k>4时,不等式knSn>bn对于一切的n∈N*恒成立.
(n+1)•2n,利用错位相减法能求出Sn=n•2n+1,要使得不等式knSn>4bn恒成立,即kn2-2n-2>0对于一切的n∈N*恒成立,由此能够证明当k>4时,不等式knSn>bn对于一切的n∈N*恒成立.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源:2012-2013学年辽宁省高三10月月考文科数学试卷(解析版) 题型:解答题
(本小题满分10分)已知函数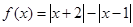
(1)试求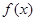 的值域;
的值域;
(2)设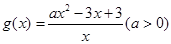 ,若对
,若对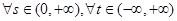 恒有
恒有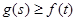 成立,试求实数
成立,试求实数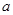 的取值氛围。
的取值氛围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com