
 、
、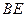 边的长分别为
边的长分别为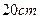 和
和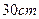 外,还特别要求包装盒必需满足:①平面
外,还特别要求包装盒必需满足:①平面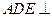 平面
平面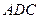 ;②平面
;②平面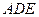 与平面
与平面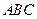 所成的二面角不小于
所成的二面角不小于 ;③包装盒的体积尽可能大。
;③包装盒的体积尽可能大。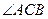 与
与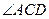 均为直角且
均为直角且 长
长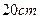 ,矩形
,矩形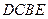 的一边长为
的一边长为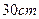 ,请你判断该包装盒的设计是否能符合客户的要求?说明理由.
,请你判断该包装盒的设计是否能符合客户的要求?说明理由.
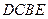 为矩形,
为矩形,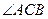 与
与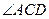 均为直角,
均为直角,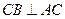 且
且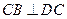 ∴
∴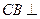 面
面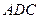 ,
,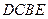 中,
中,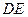 ∥
∥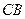
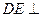 面
面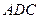 ∴面
∴面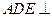 面
面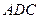 ………………………………………………3分
………………………………………………3分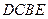 的一边长为
的一边长为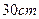 ,
,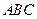 的斜边
的斜边 长为
长为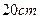 ,∴
,∴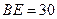
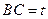 ,则
,则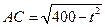 ,
,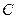 为原点,
为原点,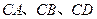 分别为
分别为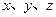 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系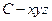 ,
,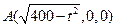 ,
,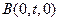 ,
,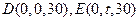 ,
,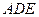 的一个法向量为
的一个法向量为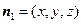 ,
,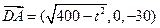 ,
,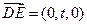
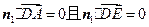
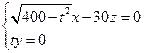 ,取
,取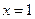 ,则
,则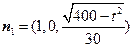 ………………………6分
………………………6分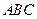 的一个法向量为
的一个法向量为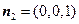 ,
,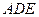 与面
与面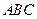 所成的二面角为
所成的二面角为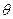 ,则
,则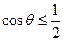 ,
,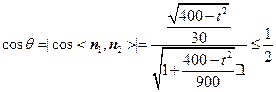 , ∴
, ∴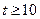 ,
,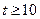 时,面
时,面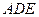 与面
与面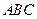 所成的二面角不小于
所成的二面角不小于 . ……………………………8分
. ……………………………8分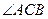 与
与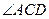 均为直角知,
均为直角知,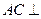 面
面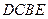 ,该包装盒可视为四棱锥
,该包装盒可视为四棱锥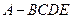 ,
,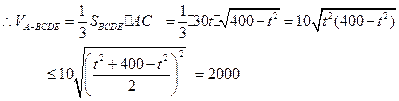
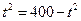 ,即
,即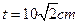 时,
时,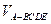 的体积最大,最大值为
的体积最大,最大值为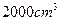 . …………………………………………………………………………………12分
. …………………………………………………………………………………12分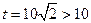 ,可以满足面
,可以满足面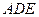 与面
与面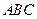 所成的二面角不小于
所成的二面角不小于 的要求,
的要求,

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:单选题
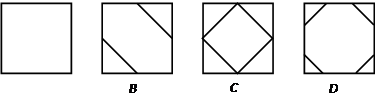
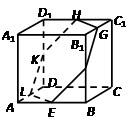
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 A的延长线于点F. 求证:
A的延长线于点F. 求证: 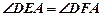 ;
;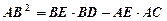

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com