
下列四个命题中,所有真命题的序号是 .
①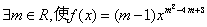 是幂函数;
是幂函数;
②若函数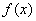 满足
满足 ,则函数
,则函数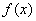 周期为2;
周期为2;
③如果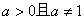 ,那么
,那么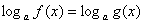 的充要条件是
的充要条件是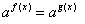 ;
;
④命题“ ”的否定是“
”的否定是“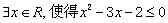 ”.
”.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
某国庆纪念品,每件成本为30元,每卖出一件产品需向税务部门上缴a元(a为常数,4≤a≤6)的税收.设每件产品的售价为x元,根据市场调查,当35≤x≤40时日销售量与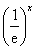 (e为自然对数的底数)成正比.当40≤x≤50时日销售量与
(e为自然对数的底数)成正比.当40≤x≤50时日销售量与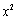 成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
(1)求L(x)关于x的函数关系式;
(2)当每件产品的售价x为多少元时,才能使L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了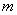 位工人某天独立生产该产品的数量,产品数量的分组区间为
位工人某天独立生产该产品的数量,产品数量的分组区间为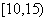 ,
,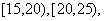

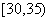 ,频率分布直方图如图所示,已知独立生产的产品数量在
,频率分布直方图如图所示,已知独立生产的产品数量在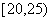 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求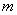 ;
;
(Ⅱ)工厂规定:若独立生产能力当日不小于25,则该工人当选今日“生产之星”.
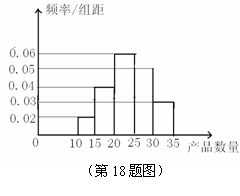 若将这天独立生产该产品数量的频率视为概率,随机从全厂工人中抽取3人,
若将这天独立生产该产品数量的频率视为概率,随机从全厂工人中抽取3人,
这3人中当日“生产之星”人数为X,求X的分布列及数学期望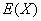 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com