
【题目】已知:以点![]()
![]() 为圆心的圆与
为圆心的圆与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() 、
、![]() ,其中
,其中![]() 为原点.
为原点.
(![]() )求证:
)求证: ![]() 的面积为定值.
的面积为定值.
(![]() )设直线
)设直线![]() 与圆
与圆![]() 交于点
交于点![]() 、
、![]() ,若
,若![]() ,求:圆
,求:圆![]() 的方程.
的方程.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)因为圆C过原点,利用两点间的距离公式表示出出O到C的距离即为圆的半径,然后根据点C的坐标,写出圆C的标准方程,令x=0,解出相应y的值,令y=0解出相应x的值,进而表示出点A和点B的坐标,利用三角形的面积公式表示出三角形AOB的面积,约分后得到面积为定值,得证;
(2)根据圆上的点到圆心的距离相等得到|CM|=|CN|,又因为|OM|=|ON|,得到OC垂直平分线段MN,由已知直线的斜率,利用两直线垂直时斜率的乘积为-1,求出直线OC的斜率,然后利用C的坐标表示出斜率,两者相等得到关于t的方程,求出方程的解得到t的值,然后把求出的t的值代入点C的坐标中确定出圆心的坐标和圆的半径,利用点到直线的距离公式判断圆心到已知直线的距离小于半径即已知直线与圆相交,把不符合题意的t舍去,得到满足题意的t的值,进而得到圆C的方程;
试题解析:(1)∵圆C过原点O,∴OC2=t2+![]() ,
,
则圆C的方程为(x-t)2+(y-![]() )2= t2+
)2= t2+![]() ,令x=0,,得y1=0,
,令x=0,,得y1=0,![]() ;
;
令y=0得x1=0,x2=2t,
即A(2t,0),B(0,![]() ),
),
![]() =4.
=4.
即△OAB的面积为定值;
(2)∵|OM|=|ON|,|CM|=|CN|,∴OC垂直平分线段MN.
∵KMN=-2,∴KOC=![]()
![]() ,解得t=2或t=-2.
,解得t=2或t=-2.
当t=2时,圆心C的坐标为(2,1)半径OC=![]() ,
,
此时圆心到直线y=-2x+4的距离d=![]() ,
,
即圆C与直线y=-2x+4相交于两点.
当t=-2时,圆心C的坐标为(-2,-1)半径OC=![]()
此时圆心到直线y=-2x+4的距离d=![]() ,即圆C与直线y=-2x+4不相交,<BR>∴t=-2不合题意,舍去.
,即圆C与直线y=-2x+4不相交,<BR>∴t=-2不合题意,舍去.
∴圆C的方程为(x-2)2+(y-1)2=5.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称,圆心
对称,圆心![]() 在第二象限,半径为
在第二象限,半径为![]() .
.
(Ⅰ)求圆![]() 的方程.
的方程.
(Ⅱ)是否存在直线![]() 与圆
与圆![]() 相切,且在
相切,且在![]() 轴、
轴、![]() 轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由.
轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a,b,c分别是角A,B,C的对边,且a=80,b=100,A= ![]() ,则此三角形是( )
,则此三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角或钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A′B′C′D′. 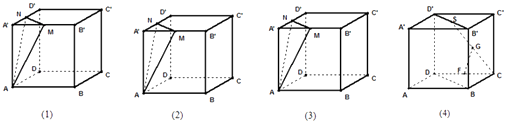
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以坐标原点为极点,
),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)讨论直线![]() 与圆
与圆![]() 的公共点个数;
的公共点个数;
(Ⅱ)过极点作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求点
,求点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长.
相交所得弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
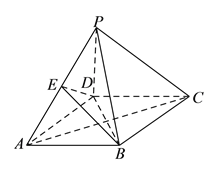
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 的交点记为
的交点记为![]() ,求证
,求证![]() 平面
平面![]() ;
;
(3)在(2)的条件下求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com