Question

解下列关于x的不等式：
（1）x³-3x²+2x＜0；
（2）

mx2

mx-1

＞x，其中m∈R．

Answer 1

分析：（1）把不等式左边的多项式提取x，再利用十字相乘的方法分解因式，变为积的形式，根据题意画出图形，利用图形即可得到原不等式的解集；
（2）分三种情况考虑：当m等于0时，把m=0代入原不等式，求出x的范围，得到原不等式的解集；当m大于0时，把不等式右边移项到左边，通分后，根据两数相乘同号得正的取符号法则化为两个不等式组，求出两不等式组的解集的并集可得到此时不等式的解集；当m小于0时，移项通分后，同理可化为两个不等式组，求出两不等式组解集的并集，得到此时不等式的解集．

解答：解：（1）x³-3x²+2x＜0，
分解因式得：x（x-1）（x-2）＜0，
画出图形如下：

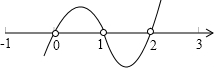
则不等式的解集为{x|x＜0或1＜x＜2}；
（2）

mx2

mx-1

＞x，
当m=0时，不等式的解集为x＜0；
当m＞0，不等式变形为：

x

mx-1

＞0，
可化为：

x＞0 mx-1＞0

或

x＜0 mx-1＜0

，
解得：x＞

1

m

或x＜0；
当m＜0时，不等式变形为：

x

mx-1

＜0，即

x

-mx+1

＞0，
可化为：

x＞0 -mx+1＞0

或

x＜0 -mx+1＜0

，
解得：x＞0或x＜

1

m

．

点评：此题考查了其他不等式的解法，利用了数形结合及分类讨论的数学思想，是高考中常考的题型．其中转化的理论依据是两数相乘同号得正，异号得负的取符号法则．