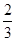练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某射手每次射击击中目标的概率均为，且每次射击的结果互不影响
    （I）假设这名射手射击3次，求至少2次击中目标的概率
    （II）假设这名射手射击3次，每次击中目标10分，未击中目标得0分，在3次射击中，若有两次连续击中目标，而另外一次未击中目标，则额外加5分；若3次全部击中，则额外加10分。用随机变量§表示射手射击3次后的总得分，求§的分布列和数学期望。
    （I）
    （II）故的分布列是

    		0
    		10
    		20
    		25
    		40







    试题分析：解：⑴设为射手3次射击击中目标的总次数，则.
    故,
    所以所求概率为.
    ⑵由题意可知，的所有可能取值为,
    用表示事件“第次击中目标”，
    则，
    ，
    ，
    ，
    .
    故的分布列是

    		0
    		10
    		20
    		25
    		40






    .
    点评：本题主要考查n次独立重复实验中恰好发生k次的概率，离散型随机变量的数学期望的求法，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    一个口袋中有红球3个，白球4个．
    （Ⅰ）从中不放回地摸球，每次摸2个，摸到的2个球中至少有1个红球则中奖，求摸2次恰好第2次中奖的概率；
    （Ⅱ）每次同时摸2个，并放回，摸到的2个球中至少有1个红球则中奖，连续摸4次，求中奖次数X的数学期望E(X)．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知随机变量X～N(1,4)且P(X<2)＝0.72，则P(1<X<2)等于(　　)．
    A．0.36 B．0.16 C．0.22D．0.28

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

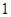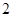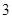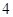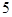    从分别写有，，，，的五张卡片中任取两张，假设每张卡片被取到的概率相等，且每张卡片上只有一个数字，则取到的两张卡片上的数字之和为偶数的概率为(    )
    A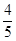．B．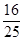
    C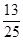．D．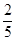

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究，他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数，得到如下资料：
    时间
    		第一天
    		第二天
    		第三天
    		第四天
    温差（℃）
    		9
    		10
    		8
    		11
    发芽数（粒）
    		33
    		39
    		26
    		46
    （1）求这四天浸泡种子的平均发芽率；
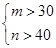    （2）若研究的一个项目在这四天中任选2天的种子发芽数来进行，记发芽的种子数分别为m，n（m＜n），则以（m，n）的形式列出所有的基本事件，并求“m，n满足”的事件A的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物)：
    61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
    (1)完成频率分布表；
    (2)作出频率分布直方图；
    (3)根据国家标准，污染指数在0～50之间时，空气质量为优；在51～100之间时，为良；在101～150之间时，为轻微污染；在151～200之间时，为轻度污染．
    请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在区间内随机取个实数，则直线，直线与轴围成的面积大于的概率是（  ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

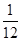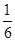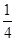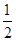    下图是某游戏中使用的材质均匀的圆形转盘，其中Ⅰ，Ⅱ，Ⅲ，Ⅳ部分的面积各占转盘面积的，，，．游戏规则如下：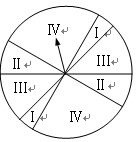

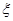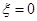    ① 当指针指到Ⅰ，Ⅱ， Ⅲ，Ⅳ部分时，分别获得积分100分，40分，10分，0分；
    ② （ⅰ）若参加该游戏转一次转盘获得的积分不是40分，则按①获得相应的积分，游戏结束；
    （ⅱ）若参加该游戏转一次获得的积分是40分，则用抛一枚质地均匀的硬币的方法来决定是否继续游戏．正面向上时，游戏结束；反面向上时，再转一次转盘，若再转一次的积分不高于40分，则最终积分为0分，否则最终积分为100分，游戏结束．
    设某人参加该游戏一次所获积分为．
    （1）求的概率；
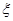    （2）求的概率分布及数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知A，B，C，D，E，F是边长为1的正六边形的6个顶点，在顶点取自A，B，C，D，E，F的所有三角形中，随机(等可能)取一个三角形．设随机变量X为取出三角形的面积．
    (Ⅰ) 求概率P ( X＝)；
    (Ⅱ) 求数学期望E ( X )．

    查看答案和解析>>

    同步练习册答案