
| ֧�� | ��֧�� | ����ν | |
| ���� | 480 | m | 180 |
| �� | 240 | 150 | 90 |
���� ����������ɵ�$\frac{480+240}{480+240+m+150+180+90}$=$\frac{24}{50}$���ⷽ�̿ɵã�
�����ɷֲ������֪�����ȡ��6����4��2Ů����6���������ȡ2�˹�15�ַ�����������1����Ů�Ե���9�֣����ݸ��ʹ�ʽ���㼴�ɣ�
��� �⣺����������ɵ�$\frac{480+240}{480+240+m+150+180+90}$=$\frac{24}{50}$��
�ⷽ�̿ɵ�m=360��
�����ɷֲ������֪�����ȡ��6����4��2Ů����4��������A��B��C��D��ʾ��Ů����a��b��ʾ��
��6���������ȡ2�˵Ļ����¼�ΪAB��AC��AD��Aa��Ab��BC��BD��Ba��Bb��CD��Ca��Cb��Da��Db��ab��15�֣�
������2��������1����Ů�Ե���Aa��Ab��Ba��Bb��Ca��Cb��Da��Db��ab��9�֣�
����2��������1����Ů�Եĸ�P=$\frac{9}{15}$=$\frac{3}{5}$
���� ���⿼��ŵ���ͼ�����ʹ�ʽ���漰�ֲ�������������⣮


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ƽ��$\frac{��}{4}$����λ���� | B�� | ����ƽ��$\frac{��}{4}$����λ���� | ||
| C�� | ����ƽ��$\frac{��}{8}$����λ���� | D�� | ����ƽ��$\frac{��}{8}$����λ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
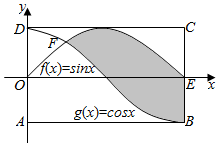 ��ͼ������ABCD���ĸ����������ֱ�ΪA��0��-1����B���У�-1����C���У�1����D��0��1������������f��x��=sinx����������g��x��=cosx�ھ���ABCD�ڽ��ڵ�F����ͼ����Ӱ���ֵ����Ϊ��������
��ͼ������ABCD���ĸ����������ֱ�ΪA��0��-1����B���У�-1����C���У�1����D��0��1������������f��x��=sinx����������g��x��=cosx�ھ���ABCD�ڽ��ڵ�F����ͼ����Ӱ���ֵ����Ϊ��������| A�� | $\sqrt{2}$+1 | B�� | $\sqrt{2}$-1 | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 72n+1 | B�� | 22n+1 | C�� | 32n+1 | D�� | 52n+1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com