练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知数列Sn为等比数列{an}的前n项和，S8=2，S24=14，则S2016=（　　）
    A．2252-2B．2253-2C．21008-2D．22016-2

    分析 由Sn为等比数列{an}的前n项和，由前n项和公式求得a1和q的数量关系，然后再来解答问题．

    解答 解：∵数列Sn为等比数列{an}的前n项和，S8=2，S24=14，
    ∴$\frac{{a}_{1}（1-{q}^{8}）}{1-q}$=2，①
    $\frac{{a}_{1}（1-{q}^{24}）}{1-q}$=14，②
    由②÷①得到：q8=2或q8=-3（舍去），
    ∴$\frac{{a}_{1}（1-2）}{1-q}$=2，
    则a1=2（q-1），
    ∴S2016=$\frac{{a}_{1}（1-{q}^{2016}）}{1-q}$=$\frac{2（q-1）（1-{q}^{{8}^{252}）}}{1-q}$=2253-2．
    故选：B．

    点评 本题考查了等边数量的前n项和，熟练掌握等比数列的性质是解题的关键，注意：本题中不需要求得首项和公比的具体数值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

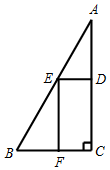    18．如图，在∠ABC=60°，∠C=90°，BC=40米的直角三角形地块中划出一块矩形CDEF地块进行绿化．
    （1）若要使矩形地块的面积不小于300$\sqrt{3}$平方米，求CF长的取值范围；
    （2）当矩形地块面积最大时，现欲修建一条道路MN，把矩形地块分成面积为1：3的两部分，且点M在边CF上，点N在边CD上，求MN的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．集合M={x|y=$\sqrt{x-3}$+$\sqrt{3-x}$}，N={y|y=$\sqrt{x-3}$•$\sqrt{3-x}$} 则下列结论正确的是（　　）
    A．M=NB．M∩N={3}C．M∪N={0}D．M∩N=∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知数列{an}的前n项和为An，对任意n∈N*满足$\frac{{{A_{n+1}}}}{n+1}$-$\frac{A_n}{n}$=$\frac{1}{2}$，且a1=1，数列{bn}满足bn+2-2bn+1+bn=0（n∈N*），b3=5，其前9项和为63．
    （1）求数列{an}和{bn}的通项公式；
    （2）令cn=$\frac{b_n}{a_n}$+$\frac{a_n}{b_n}$，数列{cn}的前n项和为Tn，若对任意正整数n，都有Tn≥2n+a，求实数a的取值范围；
    （3）将数列{an}，{bn}的项按照“当n为奇数时，an放在前面；当n为偶数时，bn放在前面”的要求进行“交叉排列”，得到一个新的数列：a1，b1，b2，a2，a3，b3，b4，a4，a5，b5，b6，…，求这个新数列的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设m，n是两条不同的直线，α，β是两个不同的平面，下列命题是真命题的是（　　）
    A．若m∥α，m∥β，则α∥βB．若m∥α，α∥β，则m∥βC．若m?α，m⊥β，则α⊥βD．若m?α，α⊥β，则m⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．a，b为正数，给出下列命题：
    ①若a2-b2=1，则a-b＜1；
    ②若$\frac{1}{b}$-$\frac{1}{a}$=1，则a-b＜1；
    ③ea-eb=1，则a-b＜1；
    ④若lna-lnb=1，则a-b＜1．
    其中真命题的有①③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．在平面直角坐标系中，已知两点A（2，-1）和B（-1，5），点P满足$\overrightarrow{AP}$=2$\overrightarrow{PB}$，则点P的坐标为（0，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．如果x＜0，0＜y＜1，那么$\frac{{y}^{2}}{x}$，$\frac{y}{x}$，$\frac{1}{x}$从小到大的顺序是$\frac{1}{x}$＜$\frac{y}{x}$＜$\frac{{y}^{2}}{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．若O为坐标原点，A（2，0），点P（x，y）坐标满足$\left\{\begin{array}{l}x-4y+3≤0\\ 3x+5y≤25\\ x≥1\end{array}$，则|$\overrightarrow{OP}$|cos∠AOP的最大值为（　　）
    A．6B．5C．4D．3

    查看答案和解析>>

    同步练习册答案