�⣺��1������{a
n}�ǡ�������С�����Ϊ��a
n=4+��n-1��•2=2n+2��
�������m��n��N
*����a
m+a
n=��2m+2��+��2n+2��=2��m+n+1��+2��
��m+n+1��N
*���ǣ���p=m+n+1������a
p=2p+2��{a
n}
��2���⣺��{a
n}�ǡ�������С����ã�������m��n��N
*���ش���p��N
*ʹa
1+��n-1��+a
1+��m-1��=a
1+��p-1��������
������a
1=p-m-n+1������
�֡�a
1��0
��a
1����������
��a
1=1��
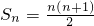
������

��
��a
1=2����

������

��
��a
1��3����

������

������

��
����������a
1=2��
��a
n=n+1��n��N
*������Ȼ���������ǡ�������С���
��3�����ۣ�����{a
n}Ϊ��������С��ij�Ҫ�����Ǵ�������m��-1��ʹa
1=md��
֤��������Ҫ�ԣ���ȡ�Ȳ����е�����a
s��a
t��s��t����������a
kʹa
s+a
t=a
k����2a
1+��s+t-2��d=a
1+��k-1��d?a
1=��k-s-t+1��d
�ʴ���m=k-s-t+1��Z��ʹa
1=md��
����֤��m��-1����d=0ʱ����Ȼ������
��d��0����m��-1����ȡp=-m��2���Բ�ͬ������a
1��a
p��
����a
qʹa
1+a
p=a
q��
��2md+��-m-1��d=md+��q-1��d?qd=0��
����q��0��d��0ì�ܣ�
�ʴ�������m��-1��ʹa
1=md��
������ԣ�����������m��-1ʹa
1=md������ȡ�Ȳ����е�����a
s��a
t��s��t����
����a
s+a
t=a
1+��s-1��d+md+��t-1��d=a
1+��s+m+t-2��d=a
s+m+t-1����s+t��3��m��-1
��s+t+m-1��������
��a
s+m+t-1��{a
n}֤�ϣ�
��������1��������֪�������m��n��N
*����a
m+a
n=��2m+2��+��2n+2��=2��m+n+1��+2����p=m+n+1����a
p=2p+2��{a
n}����������{a
n}�ǡ�������С���
��2����{a
n}�ǡ�������С����ã�������m��n��N
*���ش���p��N
*ʹa
1+��n-1��+a
1+��m-1��=a
1+��p-1��������������a
1=p-m-n+1Ϊ�������ɴ����ֽ�����������ܹ��Ƶ���a
n=n+1��n��N
*����
��3�����ۣ�����{a
n}Ϊ��������С��ij�Ҫ�����Ǵ�������m��-1��ʹa
1=md��Ȼ����֤����Ҫ�ԣ���֤������ԣ�
���������⿼���������ʵ��ۺ����ã�����ʱҪ�������⣬��ϸ���

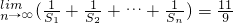 �������ڣ���{an}��ͨ�ʽ���������ڣ�˵�����ɣ�
�������ڣ���{an}��ͨ�ʽ���������ڣ�˵�����ɣ�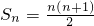 ������
������ ��
�� ������
������ ��
�� ������
������ ������
������ ��
��

