【题目】计算求值.
（1）已知cosα= 
，α为锐角，求tan2α的值；
（2）已知sin（θ+ 
）= 
，θ为钝角，求cosθ的值．
【答案】
（1）∵cosα= 
，α为锐角，
∴sinα= 
= 
，从而可求tan 
= 
∴tan2α= 
= 
=﹣ 
（2）∵sin（θ+ 
）= 
，θ为钝角，
∴θ+ ∈（ 
， 
），
∴cos（θ+ ）=﹣ 
=﹣ 
，
∴cosθ=cos[（θ+ ）﹣ ]
=cos（θ+ ）cos +sin（θ+ ）sin
=﹣ × 
+ 
=﹣ 
【解析】（1）由已知利用同角三角函数基本关系式可求sinα，进而可求tanα，利用二倍角的正切函数公式即可求tan2α的值．（2）由已知可求范围θ+ ∈（ ， ），利用同角三角函数基本关系式可求cos（θ+ ）的值，利用θ=（θ+ ）﹣ ，根据两角差的余弦函数公式即可计算得解．
【考点精析】认真审题，首先需要了解两角和与差的余弦公式(两角和与差的余弦公式：
)．
科目：高中数学 来源： 题型：
【题目】从某学校高三年级共800名男生中随机抽取50人测量身高．数据表明，被测学生身高全部介于155cm到195cm之间，将测量结果按如下方式分成八组：第一组[155，160）；第二组[160，165）；…；第八组[190，195]．如图是按上述分组方法得到的频率分布直方图的一部分．已知第一组与第八组人数相同，第六组比第七组少1人．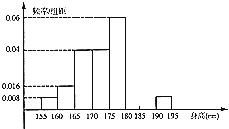 
（1）估计这所学校高三年级全体男生身高在180cm以上（含180cm）的人数；
（2）若从身高属于第六组和第八组的所有男生中随机抽取两人，记他们的身高分别为x，y，求满足“|x﹣y|≤5”的事件的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合A={（x，y）|（x﹣4）2+y2=1}，B={（x，y）|（x﹣t）2+（y﹣at+2）2=1}，如果命题“t∈R，A∩B≠”是真命题，则实数a的取值范围是（ ）
A.[1，4]
B.[0， 
]
C.[0， 
]
D.（﹣∞，0]∪（ ，+∞]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在△ABC中，∠BAC=120°，AC=3，△ABC的面积等于 
，D为边长BC上一点．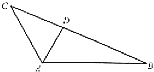 
（1）求BC的长；
（2）当AD= 
时，求cos∠CAD的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设关于x的一元二次方程x2+2ax+b2=0．
（1）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率．
（2）若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分为16分）为了保护环境，发展低碳经济，某单位在国家科研部门的支持下，进行技术攻关，新上了把二氧化碳处理转化为一种可利用的化工产品的项目，经测算，该项目月处理成本y（元）与月处理量x（吨）之间的函数关系可近似地表示为：
，且每处理一吨二氧化碳得到可利用的化工产品价值为200元，若该项目不获利，国家将给予补偿．
（1）当x∈[200,300]时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则国家每月至少需要补贴多少元才能使该项目不亏损？
（2）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线 
﹣ 
=1与直线y=2x+m有两个交点，则m的取值范围是（ ）
A.（﹣∞，﹣4）∪（4，+∞）
B.（﹣4，4）
C.（﹣∞，﹣3）∪（3，+∞）
D.（﹣3，3）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
