
 вЛДЮПМЪджаЃЌЮхУћбЇЩњЕФЪ§бЇЁЂЮяРэГЩМЈШчЯТБэЫљЪОЃК
вЛДЮПМЪджаЃЌЮхУћбЇЩњЕФЪ§бЇЁЂЮяРэГЩМЈШчЯТБэЫљЪОЃК| бЇЩњ | A1 | A2 | A3 | A4 | A5 |
| Ъ§бЇ | 89 | 91 | 93 | 95 | 97 |
| ЮяРэ | 87 | 89 | 89 | 92 | 93 |
ЗжЮі ЃЈ1ЃЉгУСаОйЗЈПЩЕУДг5УћбЇЩњжаШЮШЁ2УћбЇЩњЕФЫљгаЧщПіКЭЦфжажСЩйгавЛШЫЮяРэГЩМЈИпгк90ЃЈЗжЃЉЕФЧщПіАќКЌЕФЪТМўЪ§ФПЃЌгЩЙХЕфИХаЭЙЋЪНЃЌМЦЫуПЩЕУД№АИЃЎ
ЃЈ2ЃЉАбЫљИјЕФЮхзщЪ§ОнзїЮЊЮхИіЕуЕФзјБъУшЕНжБНЧзјБъЯЕжаЃЌЕУЕНЩЂЕуЭМЃЛИљОнЫљИјЕФЪ§ОнЯШзіГіЪ§ОнЕФЦНОљЪ§ЃЌМДбљБОжааФЕуЃЌИљОнзюаЁЖўГЫЗЈзіГіЯпадЛиЙщЗНГЬЕФЯЕЪ§ЃЌаДГіЯпадЛиЙщЗНГЬЃЎ
НтД№ НтЃКЃЈ1ЃЉДг5УћбЇЩњжаШЮШЁ2УћбЇЩњЕФЫљгаЧщПіЮЊЃК
ЃЈA4ЃЌA5ЃЉЁЂЃЈA4ЃЌA1ЃЉЁЂЃЈA4ЃЌA2ЃЉЁЂЃЈA4ЃЌA3ЃЉЁЂЃЈA5ЃЌA1ЃЉЁЂ
ЃЈA5ЃЌA2ЃЉЁЂЃЈA5ЃЌA3ЃЉЁЂЃЈA1ЃЌA2ЃЉЁЂЃЈA1ЃЌA3ЃЉЁЂЃЈA2ЃЌA3ЃЉЙВжжЧщ10ПіЃЎ
ЦфжажСЩйгавЛШЫЮяРэГЩМЈИпгк90ЃЈЗжЃЉЕФЧщПігаЃК
ЃЈA4ЃЌA5ЃЉЁЂЃЈA4ЃЌA1ЃЉЁЂЃЈA4ЃЌA2ЃЉЁЂЃЈA4ЃЌA3ЃЉЁЂЃЈA5ЃЌA1ЃЉЁЂ
ЃЈA5ЃЌA2ЃЉЁЂЃЈA5ЃЌA3ЃЉЙВ7жжЧщПіЃЌ
ЙЪЩЯЪіГщШЁЕФ5ШЫжабЁ2ШЫЃЌбЁжаЕФбЇЩњЕФЮяРэГЩМЈжСЩйгавЛШЫЕФГЩМЈИпгк9ЃЈ0ЗжЃЉЕФИХТЪP=$\frac{7}{10}$
ЃЈ2ЃЉПЩЧѓЕУЃК$\overline{x}$=$\frac{1}{5}$ЃЈ89+91+93+95+97ЃЉ=93ЃЌ$\overline{y}$=$\frac{1}{5}$ЃЈ87+89+89+92+93ЃЉ=90ЃЌ
$\sum_{i=1}^{n}{ЃЈx}_{i}-\overline{x}ЃЉ^2$=40ЃЌ$\sum_{i=1}^{n}ЃЈ{y}_{i}-\overline{y}ЃЉ^2$=24ЃЌ$\sum_{i=1}^{n}ЃЈ{x}_{i}-\overline{x}ЃЉЃЈ{y}_{i}-\overline{y}ЃЉ$=30ЃЌ
r=$\frac{\sum_{i=1}^{n}{ЃЈx}_{i}-\overline{x}ЃЉЃЈ{y}_{i}-\overline{y}ЃЉ}{\sqrt{\sum_{i=1}^{n}ЃЈ{x}_{i-}\overline{x}ЃЉ^2\sum_{i=1}^{n}ЃЈ{y}_{i}-\overline{y}ЃЉ^2}}$=$\frac{30}{\sqrt{40ЁС24}}$Ёж$\frac{30}{30.97}$Ёж0.97ЃЌ
ПЩвдПДГіЃЌЮяРэГЩМЈгыЪ§бЇГЩМЈИпЖШе§ЯрЙиЃЌ
ЩЂЕуЭМШчЭМЫљЪОЃЎ
ЩшЛиЙщжБЯпЕФЗНГЬЃК$\widehat{y}$=$\widehat{b}x+\widehat{a}$ЃЌ
дђ$\hat{b}$=$\frac{\sum_{i=1}^{n}ЃЈ{x}_{i}-\overline{x}ЃЉЃЈ{y}_{i}-\overline{y}ЃЉ}{\sum_{i=1}^{n}ЃЈ{x}_{i}-\overline{x}ЃЉ^2}$=0.75ЃЌ$\widehat{a}=\widehat{y}-\widehat{b}x$=20.25ЃЌ
ЙЪyЙигкxЕФЯпадЛиЙщЗНГЬЪЧЃК$\hat{y}$=0.75x+20.25
ЕуЦР БОЬтжївЊПМВщСЫЙХЕфИХаЭКЭЯпадЛиЙщЗНГЬЕШжЊЪЖЃЌПМВщСЫбЇЩњЕФЪ§ОнДІРэФмСІКЭгІгУвтЪЖЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ГфЗжЖјВЛБивЊЬѕМў | BЃЎ | БивЊЖјВЛГфЗжЬѕМў | ||
| CЃЎ | ГфЗжБивЊЬѕМў | DЃЎ | МШВЛГфЗжвВВЛБивЊЬѕМў |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт

| AЃЎ | 120 | BЃЎ | 720 | CЃЎ | 1440 | DЃЎ | 5040 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
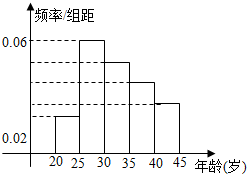 ФГОгУёаЁЧјФъСфдк20ЫъЕН45ЫъЕФОгУёЙВга150ШЫЃЌШчЭМЪЧЫћУЧЩЯЭјЧщПіЕФЦЕТЪЗжВМжБЗНЭМЃЌЯжвбжЊФъСфдк[30ЃЌ35ЃЉЃЌ[40ЃЌ45]ЕФШЫЪ§ЗжБ№ЪЧ39ЁЂ21ШЫЃЌдђФъСфдк[35ЃЌ40ЃЉЕФЦЕЪ§ЃЈЁЁЁЁЃЉ
ФГОгУёаЁЧјФъСфдк20ЫъЕН45ЫъЕФОгУёЙВга150ШЫЃЌШчЭМЪЧЫћУЧЩЯЭјЧщПіЕФЦЕТЪЗжВМжБЗНЭМЃЌЯжвбжЊФъСфдк[30ЃЌ35ЃЉЃЌ[40ЃЌ45]ЕФШЫЪ§ЗжБ№ЪЧ39ЁЂ21ШЫЃЌдђФъСфдк[35ЃЌ40ЃЉЕФЦЕЪ§ЃЈЁЁЁЁЃЉ| AЃЎ | 6 | BЃЎ | 9 | CЃЎ | 30 | DЃЎ | 45 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com