练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
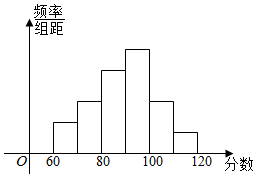
    19．为了了解高三学生的数学成绩，抽取了某班60名学生，将所得数据整理后，画出如图所示的频率分布直方图，已知从左到右各长方形高的比为2：3：5：6：3：1，则该班学生数学成绩在[100，120]之间的学生人数是（　　）
    A．32B．24C．18D．12

    分析 设从左到右各长方形高的比为2k，3k，5k，6k，3k，k，由频率分布直方图的性质求出k=0.05，再求出该班学生数学成绩在[100，120]之间的学生频率，由此能求出该班学生数学成绩在[100，120]之间的学生人数．

    解答 解：∵从左到右各长方形高的比为2：3：5：6：3：1，
    ∴设从左到右各长方形高的比为2k，3k，5k，6k，3k，k，
    由频率分布直方图的性质得：
    2k+3k+5k+6k+3k+k=1，解得k=0.05，
    ∴该班学生数学成绩在[100，120]之间的学生频率为：
    3k+k=4k=4×0.05=0.2，
    ∴该班学生数学成绩在[100，120]之间的学生人数是60×0.2=12（人）．
    故选：D．

    点评 本题考查该班学生数学成绩在[100，120]之间的学生人数的求法，是基础题，解题是要认真审题，注意频率分布直方图的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．下列各角中与-$\frac{π}{4}$终边相同的是（　　）
    A．-$\frac{3π}{4}$B．$\frac{π}{4}$C．$\frac{7π}{4}$D．$\frac{3π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

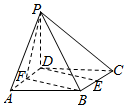    10．如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E，F分别为棱BC，AD的中点．
    （Ⅰ）若PD=1，求异面直线PB和DE所成角的余弦值．
    （Ⅱ）若二面角P-BF-C的余弦值为$\frac{\sqrt{6}}{6}$，求四棱锥P-ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（x，1），$\overrightarrow{u}$=$\overrightarrow{a}$+2$\overrightarrow{b}$，$\overrightarrow{v}$=2$\overrightarrow{a}$-$\overrightarrow{b}$．
    （Ⅰ）当$\overrightarrow{u}$∥$\overrightarrow{v}$时，求x的值；
    （Ⅱ）当$\overrightarrow{u}$⊥$\overrightarrow{v}$时且x＜0时，求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角α．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．以正三棱柱的顶点为顶点的四面体共有12个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．国Ⅳ标准规定：轻型汽车的屡氧化物排放量不得超过80mg/km．根据这个标准，检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆，对其氮氧化物的排放量进行检测，检测结果记录如表（单位：mg/km）
    A8580856090
    B70x95y75
    由于表格被污损，数据x，y看不清，统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等，方差也相等．
    （1）求表格中x与y的值；
    （2）从被检测的5辆B种型号的出租车中任取2辆，记“氮氧化物排放量超过80mg/km”的车辆数为X，求X=1时的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知集合A={x|ax2-2x+1=0}
    （1）若A中有两个元素，求a的取值范围；
    （2）若A中至少有一个元素，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

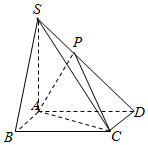    15．如图，在四棱锥S-ABCD中，底面ABCD为矩形，SA⊥平面ABCD，AB=1，AD=AS=2，P是棱SD上一点，且$SP=\frac{1}{2}PD$．
    （1）求直线AB与CP所成角的余弦值；
    （2）求二面角A-PC-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．定义max{a，b}=$\left\{\begin{array}{l}{a，a≥b}\\{b，a＜b}\end{array}\right.$，若实数x，y满足$\left\{\begin{array}{l}{-1≤x≤1}\\{-1≤y≤1}\end{array}\right.$，则max{2x+1，x-2y+5}的最小值为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案