
分析 (1)由于A中有两个元素,可得方程a≠0,ax2-2x+1=0有两个实数根,因此△>0,解出即可得出.
(2)对a分类讨论,利用方程的解与判别式的关系即可得出.
解答 解:(1)∵A中有两个元素,
∴a≠0,方程ax2-2x+1=0有两个实数根,
∴△=4-4a>0,a≠0,
解得a<1,且a≠0.
∴a的取值范围是(-∞,0)∪(0,1).
(2)当a=0时,ax2-2x+1=0化为:-2x+1=0,解得x=$\frac{1}{2}$,此时A=$\{-\frac{1}{2}\}$.
当a≠0时,ax2-2x+1=0有实数根,则△=4-4a≥0,解得a≤1,且a≠0.
综上可得:实数a的取值范围是(-∞,1].
点评 本题考查了集合的运算性质、一元二次方程的实数根与判别式的关系、不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
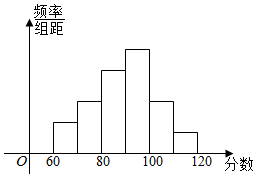 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出如图所示的频率分布直方图,已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[100,120]之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出如图所示的频率分布直方图,已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[100,120]之间的学生人数是( )| A. | 32 | B. | 24 | C. | 18 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
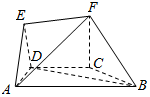 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
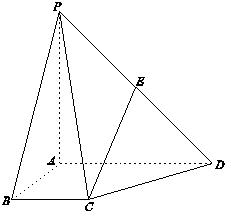 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PA=AB=AD=2BC=2,∠BAD=θ,E是PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PA=AB=AD=2BC=2,∠BAD=θ,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
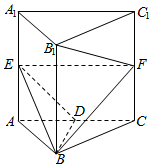 三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D、E、F分别是棱AC,AA1,CC1的中点
三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D、E、F分别是棱AC,AA1,CC1的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
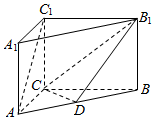 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=AA1=4,AC⊥BC,D是线段AB上一点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=AA1=4,AC⊥BC,D是线段AB上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com