
分析 (1)根据若$\overrightarrow{AB}$⊥$\overrightarrow{a}$,转化为$\overrightarrow{AB}$•$\overrightarrow{a}$=0,解方程即可.
(2)根据向量$\overrightarrow{AC}$与向量$\overrightarrow{a}$共线,建立方程关系,转化为一元二次函数进行求解.
解答 解:(Ⅰ)$\overrightarrow{AB}=(-16,t),\overrightarrow a=(1,2)$
∵$\overrightarrow{AB}$⊥$\overrightarrow{a}$,
∴$\overrightarrow{AB}$•$\overrightarrow{a}$=0,即-16+2t=0,得t=8
故$\overrightarrow{OB}=(-8,8)$…(6分)
(Ⅱ)∵向量$\overrightarrow{AC}$与向量$\overrightarrow{a}$共线,$\overrightarrow{AC}=(8sinθ-8,t)$,$\overrightarrow a=(1,2)$
∴$\frac{8sinθ-8}{1}=\frac{t}{2}$,得t=16sinθ-16…(8分),
$tsinθ=16{sin^2}θ-16sinθ=16{(sinθ-\frac{1}{2})^2}-4$
故当sinθ=$\frac{1}{2}$时,tsinθ取最小值4,…(10分)
此时$\overrightarrow{OC}=(4,-8)$,
则$\overrightarrow{OA}•\overrightarrow{OC}=(8,0)•(4,-8)=32$.
点评 本题主要考查向量数量积的应用,根据向量垂直和向量关系的坐标公式是解决本题的关键.考查学生的运算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| x | 6 | 8 | 10 | 12 |
| y | 6 | m | 3 | 2 |
| A. | 可以预测,当x=9时,y=4 | B. | 该回归直线必过点(9,4) | ||
| C. | m=4 | D. | m=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
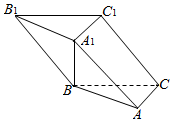 如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.
如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
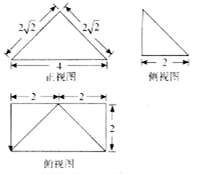 已知四棱锥P-ABCD的三视图如图所示,则此四棱锥外接球的半径为( )
已知四棱锥P-ABCD的三视图如图所示,则此四棱锥外接球的半径为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com