【答案】
分析:(1)利用等差数列{a
n}中,a
4S
4=-14,S
5-a
5=-14,可求首项与公差,从而可求求数列{a
n}的通项公式;
(2)将曲线C
n与l的方程联立,利用判别式可求解;
(3)利用(2)的结论,表达出M
n=(|a
n|+4)|A
nB
n|,再求M
n的最小值.
解答:解:(1)由题意可得S
4=s
5-a
5=-14,故a
4S
4=-14a
4=-14,即a
4=1,
设数列的公差为d,则
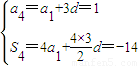
,
解得
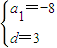
,故a
n=a
1+(n-1)d=3n-11;
(2)联立方程
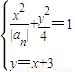
,消掉y并整理得(|an|+4)x2+6|an|x+5|an|=0,
由题意知△=16(|a
n|
2-5|a
n|)>0,即|a
n|>5,
∴3n-11>5或3n-11<-5,即n>
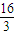
或n<2,
即n≥6或n=1时,直线l与曲线C
n相交于不同的两点.
(3)由(2)当n≥6或n=1时,直线l与曲线C
n相交于不同的两点.
M
n=(|a
n|+4)•|A
nB
n|=(|an+4|)
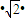
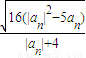
=
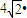

=
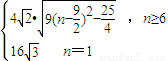
,
∴当n=6时,M
n的最小值为
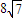 点评:
点评:本题以数列为载体,考查直线与圆锥曲线的位置关系,关键是利用直线与圆锥曲线方程联立,并借助于判别式进行解决,属中档题.

 ,直线l的方程是y=x+3.
,直线l的方程是y=x+3.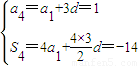 ,
,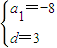 ,故an=a1+(n-1)d=3n-11;
,故an=a1+(n-1)d=3n-11;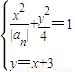 ,消掉y并整理得(|an|+4)x2+6|an|x+5|an|=0,
,消掉y并整理得(|an|+4)x2+6|an|x+5|an|=0,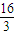 或n<2,
或n<2,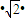
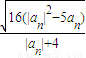
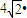
 =
=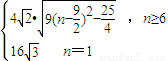 ,
,