
分析 利用函数的最值判断(1)的正误;求出函数的最值判断(2)的正误;利用函数的性质判断(3)的正误;(4)利用函数的性质判断(4)的正误.
解答 解:(1)给定区间上的单调函数一定存在最大最小值;如果区间是开区间显然不满足最值定理,所以(1)不正确;
(2)函数y=x2+3x-4在(-3,3],当x=-$\frac{3}{2}$(函数的对称轴)函数有最小值,x=3时有最大值,所以函数既有最小值又有最大值;所以(2)正确;
(3 )函数y=$\frac{1}{x}$在(一2,-1]上只有最小值,没有最大值;因为函数函数y=$\frac{1}{x}$在(一2,-1]是减函数,x=-1时有最小值,所以(3)正确;
(4)函数y=$\frac{1}{x}$在[一2,0)∪(0,2]上只有最小值,没有最大值.函数是奇函数,两个区间上都是减函数,所以(4)不正确;
故答案为:(2)(3).
点评 本题考查命题的真假的判断与应用,函数的单调性以及函数的在的求法,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,1) | B. | (-∞,-1)∪(-1,0) | C. | (-1,0)∪(0,+∞) | D. | [-1,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [1,2] | C. | [0,2] | D. | [0,3] |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北涞水波峰中学高一9月月考数学试卷(解析版) 题型:解答题
经市场调查,某门市部的一种小商品在过去的20天内的日销售量(件)与价格(元)均为时间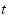 (天)的函数,且日销售量近似满足函数
(天)的函数,且日销售量近似满足函数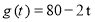 (件),而且销售价格近似满足于
(件),而且销售价格近似满足于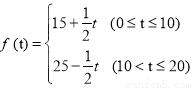 (元).
(元).
(1)试写出该种商品的日销售额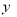 与时间
与时间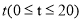 的函数表达式;
的函数表达式;
(2)求该种商品的日销售额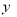 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com