
【题目】某地区2011年至2017年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求样本中心点坐标;
(2)已知两变量线性相关,求y关于t的线性回归方程;
(3)利用(2)中的线性回归方程,分析2011年至2017年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2019年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: .
.
【答案】(1)![]() ;(2)
;(2)![]() =0.5t+2.3;(3)见解析
=0.5t+2.3;(3)见解析
【解析】
(1)由表中数据计算![]() 、
、![]() 即可;
即可;
(2)由所给数据计算出回归系数,写出回归方程即可;
(3)由![]() =0.5>0知y关于t正相关,求出t=9时
=0.5>0知y关于t正相关,求出t=9时![]() 的值即可.
的值即可.
(1)由所给数据计算得
![]() (1+2+3+4+5+6+7)=4,
(1+2+3+4+5+6+7)=4,
![]() (2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
所以样本中心点为![]() .
.
(2)![]() =9+4+1+0+1+4+9=28,
=9+4+1+0+1+4+9=28,
![]() =(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
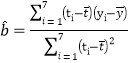 =
=![]() =0.5,
=0.5,![]() =4.3-0.5×4=2.3,
=4.3-0.5×4=2.3,
故所求线性回归方程为![]() =0.5t+2.3.
=0.5t+2.3.
(3)由(2)知,![]() =0.5>0,故2011年至2017年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.将2019年的年份代号t=9代入(2)中的线性回归方程,得
=0.5>0,故2011年至2017年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.将2019年的年份代号t=9代入(2)中的线性回归方程,得![]() =0.5×9+2.3=6.8,故预测该地区2019年农村居民家庭人均纯收入为6.8千元.
=0.5×9+2.3=6.8,故预测该地区2019年农村居民家庭人均纯收入为6.8千元.


科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①命题“若![]() ,则
,则![]() ”的逆否命题为假命题:
”的逆否命题为假命题:
②命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;
”;
③若“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,则
”为假命题,则![]() 为真命题,
为真命题,![]() 为假命题;
为假命题;
④函数![]() 有极值的充要条件是
有极值的充要条件是![]() 或
或![]() .
.
其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(l)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x﹣y=1与圆Γ:x2+y2﹣2x+2y﹣1=0相交于A,C两点,点B,D分别在圆Γ上运动,且位于直线l的两侧,则四边形ABCD面积的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(xn,yn),….
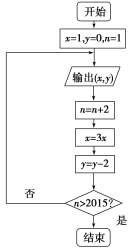
(1)若程序运行中输出的一个数组是(9,t),求t的值;
(2)程序结束时,共输出(x,y)的组数为多少;
(3)写出程序框图的程序语句.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某机构调查小学生课业负担的情况,设平均每人每天做作业时间为X(单位:分钟),按时间分下列四种情况统计:①0~30分钟;②30~60分钟;③60~90分钟;④90分钟以上,有1000名小学生参加了此项调查,如图是此次调查中某一项的程序框图,其输出的结果是600,则平均每天做作业时间在0~60分钟内的学生的频率是( )

A. 0.20B. 0.80C. 0.60D. 0.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,△ABC内接于圆O,D是 ![]() 的中点,∠BAC的平分线分别交BC和圆O于点E,F. (Ⅰ)求证:BF是△ABE外接圆的切线;
的中点,∠BAC的平分线分别交BC和圆O于点E,F. (Ⅰ)求证:BF是△ABE外接圆的切线;
(Ⅱ)若AB=3,AC=2,求DB2﹣DA2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校高二年级共2000名学生,其中男生1200人.为调查学生们的手机使用情况,采用分层抽样的方法,随机抽取100位学生每周平均使用手机上网时间的样本数据(单位:小时).根据这100个数据,得到学生每周平均使用手机上网时间的频率分布直方图(如图所示),其中样本数据分组区间分别为![]() .
.
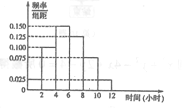
(1)应收集男生、女生样本数据各多少人?
(2)估计我校高二年级学生每周平均使用手机上网时间超过4小时的概率.
(3)将平均每周使用手机上网时间在![]() 内定义为“长时间使用手机”,在
内定义为“长时间使用手机”,在![]() 内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
近视 | 不近视 | 合计 | |
长时间使用手机上网 | |||
短时间使用手机上网 | 15 | ||
合计 | 25 |
附:![]()
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com