
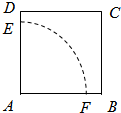
 如图,设边长为1的正方形纸片,以A为圆心,AE=a(0<a≤1)为半径画圆弧EF,裁剪的扇形AEF围成一个圆锥的侧面,余下的部分裁剪出它的底面.当圆锥的侧面积最大时,圆锥底面的半径r=
如图,设边长为1的正方形纸片,以A为圆心,AE=a(0<a≤1)为半径画圆弧EF,裁剪的扇形AEF围成一个圆锥的侧面,余下的部分裁剪出它的底面.当圆锥的侧面积最大时,圆锥底面的半径r=| 2 |
| 2 |
5
| ||
| 23 |
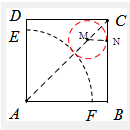 根据题意,欲在正方形ABCD内且在扇形AEF外的余下部分裁剪出圆锥的底面,
根据题意,欲在正方形ABCD内且在扇形AEF外的余下部分裁剪出圆锥的底面,| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| π |
| 2 |
| 2 |
| 2 |
5
| ||
| 23 |
| 2 |
| 2 |
5
| ||
| 23 |
5
| ||
| 23 |
5
| ||
| 23 |
5
| ||
| 23 |


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点,截面DEF∥底面ABC,且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量| AP |
| AB |
| AF |
查看答案和解析>>
科目:高中数学 来源: 题型:
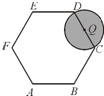 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)写出体积V与高h的函数关系式;
(2)当![]() 为多少时,体积V最大,最大值是多少?
为多少时,体积V最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二下学期数学单元测试1-理科 题型:解答题
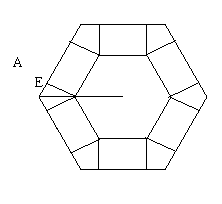
如图,把边长为a的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为h所做成的盒子体积V(不计接缝).
(1)写出体积V与高h的函数关系式;
 (2)当
(2)当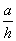 为多少时,体积V最大,最大值是多少?
为多少时,体积V最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com