
分析 (1)利用二倍角公式、两角和公式和辅助角公式将函数化为y=Asin(ωx+φ)的形式,可得函数f(x)的解析式,再利用周期公式求函数的最小正周期.
(2)当x∈[0,$\frac{π}{3}$]时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值,即得到函数f(x)的值域.
解答 解:(1)函数f(x)=sin2x-$\frac{{\sqrt{3}}}{2}$sin2x
=$\frac{1}{2}$$-\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}sin2x$
=$\frac{1}{2}-sin(2x+\frac{π}{6})$,
最小正周期$T=\frac{2π}{ω}=\frac{2π}{2}=π$;
所以函数f(x)的解析式为简$f(x)=-sin(2x+\frac{π}{6})+\frac{1}{2}$;最小正周期T=π.
(2)由(1)得知$f(x)=-sin(2x+\frac{π}{6})+\frac{1}{2}$;
当x∈[0,$\frac{π}{3}$]时,那么:$\frac{π}{6}≤2x+\frac{π}{6}≤\frac{5π}{6}$,
∴$\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$
∴$-\frac{1}{2}≤f(x)≤0$
∴函数f(x)的值域是$[{-\frac{1}{2},0}]$.
点评 本题考查了三角函数图象及性质的综合运用能力和计算能力,对三角函数的理解,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
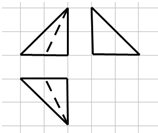 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的体积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的体积为( )| A. | 4 | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 商品销售收入与商品的广告支出经费之间具有相关关系 | |
| B. | 线性回归方程对应的直线$\hat y=\hat bx+\hat a$,至少经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com