
| A�� | ��Ʒ������������Ʒ�Ĺ��֧������֮�������ع�ϵ | |
| B�� | ���Իع鷽�̶�Ӧ��ֱ��$\hat y=\hat bx+\hat a$�����پ������������ݵ㣨x1��y1������x2��y2����������xn��yn���е�һ���� | |
| C�� | �ڲв�ͼ�У��в��ֲ��Ĵ�״����Ŀ���Խխ����ģ����ϵľ���Խ�� | |
| D�� | �ڻع�����У�R2Ϊ0.98��ģ�ͱ�R2Ϊ0.80��ģ����ϵ�Ч���� |
���� ������ع�ϵ�Ķ��壬���ж�A�����ݻع�ֱ�ߵļ������������ж�B�����ݲв�����壬���ж�C�����ݻع�ϵ�������壬���ж�D��
��� �⣺��Ʒ������������Ʒ�Ĺ��֧������֮�������ع�ϵ����A��ȷ��
���Իع鷽�̶�Ӧ��ֱ��$\hat y=\hat bx+\hat a$���Բ������κ����ݵ㣬��B����
�ڲв�ͼ�У��в��ֲ��Ĵ�״����Ŀ���Խխ����ʾ�в�ԽС����ģ����ϵľ���Խ�ߣ���C��ȷ��
�ڻع�����У�R2ֵԽ�����Ч��Խ�ã���R2Ϊ0.98��ģ�ͱ�R2Ϊ0.80��ģ����ϵ�Ч���ã���D��ȷ��
��ѡ��B��
���� ���������������ж���Ӧ��Ϊ���壬������ͳ���е���ظ���ѶȲ������ڻ����⣮


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
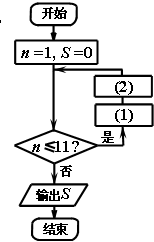 ��ͼ��Ϊ�˼���1+2+22+��+210��ֵ����Ƶij����ͼ��
��ͼ��Ϊ�˼���1+2+22+��+210��ֵ����Ƶij����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��ͳ��רҵ | ͳ��רҵ | |
| �� | 13 | 10 |
| Ů | 7 | 20 |
| P��x2��x0�� | 0.10 | 0.05 | 0.025 | 0.010 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ ${x_0}��R��{2^{x_0}}��0$ | B�� | �������${x_0}��R��{2^{x_0}}��0$ | ||
| C�� | ������� ${x_0}��R��{2^{x_0}}��0$ | D�� | ���� ${x_0}��R��{2^{x_0}}��0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | $8\sqrt{7}$ | C�� | $8\sqrt{14}$ | D�� | 16 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com