
分析 (1)对x分类讨论,去掉绝对值符号解出即可得出.
(2)当a>$\frac{1}{2}$,x∈[$\frac{1}{2}$,a],时,f(x)=4x+a-1,不等式f(x)≤g(x)化为3x≤4-a,化简利用a的取值范围即可得出.
解答 解:(1)由|2x-1|+|2x+2|<x+3,得:
①$\left\{\begin{array}{l}{x<-1}\\{-4x-1<x+3}\end{array}\right.$得x∈∅;
②$\left\{\begin{array}{l}{-1≤x≤\frac{1}{2}}\\{3<x+3}\end{array}\right.$得0<x≤$\frac{1}{2}$;
③$\left\{\begin{array}{l}{x>\frac{1}{2}}\\{4x+1<x+3}\end{array}\right.$得$\frac{1}{2}<x<\frac{2}{3}$…(5分)
综上:不等式f(x)<g(x)的解集为$(0,\frac{2}{3})$…(6分)
(2)∵a>$\frac{1}{2}$,x∈[$\frac{1}{2}$,a],
∴f(x)=4x+a-1…(7分)
由f(x)≤g(x)得:3x≤4-a,即x≤$\frac{4-a}{3}$.
依题意:[$\frac{1}{2}$,a]⊆(-∞,$\frac{4-a}{3}$]
∴a≤$\frac{4-a}{3}$即a≤1…(9分)
∴a的取值范围是($\frac{1}{2}$,1]…(10分)
点评 本题考查了绝对值不等式的解法、恒成立问题的等价转化方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
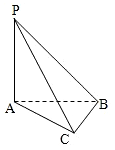 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AC=$\sqrt{2}$,则三棱锥P-ABC外接球的体积是( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AC=$\sqrt{2}$,则三棱锥P-ABC外接球的体积是( )| A. | $\frac{{\sqrt{2}π}}{3}$ | B. | $\frac{8π}{3}$ | C. | $\frac{4π}{3}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 商品销售收入与商品的广告支出经费之间具有相关关系 | |
| B. | 线性回归方程对应的直线$\hat y=\hat bx+\hat a$,至少经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com