已知:函数f(x)=-x(x-a)2 (a∈R)
(1)求a=1时曲线y=f(x)在点(2,f(2))处的切线方程
(2)当a<0时,求函数f(x)的极小值
(3)是否存在实数a,使得f(x)在[-1,1]上单调递增.若存在求出a,若不存在请说明理由.
解:(1)当a=1时,f(x)=-x(x-1)
2=-x
3+2x
2-x∴f'(x)=-3x
2+4x-1∴f'(2)=-5,f(2)=-2∴切线方程:y+2=-5(x-2),即:5x+y-8=0(4分)
(2)∵f(x)=-x(x-a)
2=-x
3+2ax
2-a
2x∴f'(x)=-3x
2+4ax-a
2=-(x-a)(3x-a)(5分)
则f(x),f'(x)的关系如下表表示:
| (-∞,a) | a |  |  | 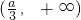 |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
∴f(x)的极小值=f(a)=0(8分)
(3)∵f(x)=-x(x-a)
2在[-1,1]上单调递增,则f'(x)=-3x
2+4ax-a
2≥0在[-1,1]恒成立 (9分)
∴
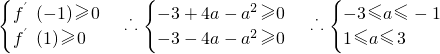
∴a无解 (13分)
综上,不存在实数a,使得f(x)在[-1,1]上单调递增 (14分)
分析:(1)当a=1时f(x)=-x
3+2x
2-x,得f′(x)=-3x
2+4x-1,当x=2时y=-2,得切点为(2,-2)得切线的斜率k=-5;
(2)f'(x)=-3x
2+4ax-a
2=-(x-a)(3x-a),再研究导数为0时,左右附近的正负情况即可;
(3)欲使f(x)在[-1,1]上单调递增,只需f′(x)≤0在[-1,1]上恒成立,利用分离法将a分离出来,求出不等式另一侧的最大值,即可求出a的范围.
点评:本题主要考查了函数恒成立问题,以及利用导数研究函数的单调性、极值等基础知识,考查计算能力和分析问题的能力.解决此类问题的方法是利用导数求出切线的斜率再求出切点即可,而解决方程有解问题时一般先转化为利用导数求函数的最值,利用最值求出参数的范围即可,高考考查的重点.



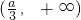
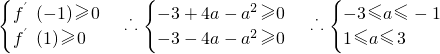 ∴a无解 (13分)
∴a无解 (13分)

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案