[题目]在△ABC中.角A.B.C的对边分别是a.b.c.若 + =2a.b= .则△ABC面积是题目和参考答案——青夏教育精英家教网—

【题目】在△ABC中，角A，B，C的对边分别是a，b，c，若 + =2a，b= ，则△ABC面积是

【答案】1
【解析】解：∵ + =2a，可得：，
∴ =2sinA，
∴sin2C+sin2B=2（sinBcosC+cosBsinC）sinBsinC=2sin2BsinCcosC+2sin2CsinBcosB，
∴sin2C（1﹣2sinBcosB）+sin2B（1﹣2sinCcosC）=0，
∴sin2C（sinB﹣cosB）2+sin2B（sinC﹣cosC）2=0，
∴sinB=cosB，sinC=cosC，可得：B=C=45°，
又∵b= ，
∴S△ABC= ×（）2=1．
所以答案是：1．
【考点精析】本题主要考查了正弦定理的定义的相关知识点，需要掌握正弦定理:才能正确解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:

日期	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
天气	晴	雨	阴	阴	阴	雨	阴	晴	晴	晴	阴	晴	晴	晴	晴
日期	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
天气	晴	阴	雨	阴	阴	晴	阴	晴	晴	晴	阴	晴	晴	晴	雨

(1)在4月份任取一天,估计西安市在该天不下雨的概率;

(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】根据所给的条件求直线的方程：

（1）直线过点（-4，0），倾斜角的正弦值为；

（2）直线过点（5，10），到原点的距离为5.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，∠BCD=135°，侧面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E，F分别为BC，AD的中点，点M在线段PD上．（Ⅰ）求证：EF⊥平面PAC；
（Ⅱ）如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等，求的值．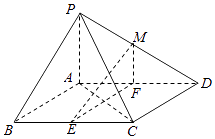

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设数列满足：．

(1)求数列的通项公式；

(2)设，求数列的前项和．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】由于被墨水污染，一道数学题仅能见到如下文字：“已知二次函数的图像经过，，求证：这个二次函数的图像关于直线对称”，根据已知消息，题中二次函数图像不具有的性质是（）．

A. 在轴上的截线段长是 B. 与轴交于点

C. 顶点 D. 过点

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知{an}是一个公差大于0的等差数列，且满足a3a6=55，a2+a7=16．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）等比数列{bn}满足：b1=a1 ， b2=a2﹣1，若数列cn=anbn ，求数列{cn}的前n项和Sn ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】有一个公益广告说：“若不注意节约用水，那么若干年后，最有一滴水只能是我们的眼泪。”我国是水资源匮乏的国家。为鼓励节约用水，某市打算出台一项水费政策措施，规定：每一季度每人用水量不超过5吨时，每吨水费收基本价1.3元；若超过5吨而不超过6吨时，超过部分的水费加收200%；若超过6吨而不超过7吨时，超过部分的水费加收400%。设某人本季度实际用水量为吨，应交水费为f(x)，（1）求的值；（2）试求出函数f(x)的解析式。