
【题目】设数列![]() 满足:
满足:![]()
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1) ;(2)
;(2)![]()
![]()
【解析】
(1)根据题意,可得a1+2a2+3a3++(n﹣1)an﹣1=2n﹣1,两者相减,可得数列{an}的通项公式;
(2)根据题意,求出bn的通项公式,利用错位相减法求出数列{bn}的前n项和Sn.
(1)∵a1+2a2+3a3+…+nan=2n①,
∴n≥2时,a1+2a2+3a3+…+(n﹣1)an﹣1=2n﹣1②
①﹣②得nan=2n﹣1,an=![]() (n≥2),在①中令n=1得a1=2,
(n≥2),在①中令n=1得a1=2,
∴an=
(2)∵bn=![]() .
.
则当n=1时,S1=2
∴当n≥2时,Sn=2+2×2+3×22+…+n×2n﹣1
则2Sn=4+2×22+3×23+…+(n﹣1)2n﹣1+n2n
相减得Sn=n2n﹣(2+22+23+…+2n﹣1)=(n﹣1)2n+2(n≥2)
又S1=2,符合Sn的形式,
∴Sn=(n﹣1)2n+2(n∈N*)


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为 (米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=4,点P为直线x+2y﹣9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( )
A.![]()
B.![]()
C.(2,0)
D.(9,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() +ax,aR,
+ax,aR,
(1)讨论函数f(x)的单调区间;
(2)求证:![]() ≥x;
≥x;
(3)求证:当a≥-2时,x[1,+ ∞),f(x)+lnx≥a+1恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
(Ⅱ)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的取值范围;
(Ⅲ)求证:ln(4n+1)≤16 ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x吨、3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求证:OE∥平面PDC;
(Ⅲ)求面PAD与面PBC所成角的大小.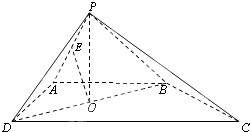
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市有一块半径为40m的半圆形绿化区域(以O为圆心,AB为直径),现对其进行改建,在AB的延长线上取点D,OD=80m,在半圆上选定一点C,改建后绿化区域由扇形区域AOC和三角形区域COD组成,其面积为Scm2 . 设∠AOC=xrad. 
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)试问∠AOC多大时,改建后的绿化区域面积S取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com