
【题目】已知函数f(x)=![]() +ax,aR,
+ax,aR,
(1)讨论函数f(x)的单调区间;
(2)求证:![]() ≥x;
≥x;
(3)求证:当a≥-2时,x[1,+ ∞),f(x)+lnx≥a+1恒成立.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】试题分析:(1)由题意,求得![]() ,根据
,根据![]() 和
和![]() ,分类讨论,即可得到函数
,分类讨论,即可得到函数![]() 的单调区间;
的单调区间;
(2)令![]() ,由(1)可知,函数
,由(1)可知,函数![]() 的最小值为
的最小值为![]() ,即可证明不等式;
,即可证明不等式;
(3)不等式![]() 恒成立转化为不等式
恒成立转化为不等式![]() ,设出函数
,设出函数![]() ,利用导数求解函数
,利用导数求解函数![]() 的最小值,即可作出证明.
的最小值,即可作出证明.
试题解析:
(1)解:fˊ(x) = ![]() +a.
+a.
(i)当a≥0时, fˊ(x)>0,函数f(x)在R上单调递增;
(ii)当 a<0 时,令fˊ(x) =0,则ln(-a)+1,
当fˊ(x)>0,即x>ln( -a) + 1时,函数f (x)单调递增;
当fˊ(x)<0,即x<ln( -a) + 1时,函数f (x)单调递减.
综上,当a≥0时,函数f (x)在R上单调递增;当a<0时,函数f (x)的单调递增区间是(ln(-a)+1,+∞), 单调递减区间是(一∞,ln(-a)十1).
(2)证明:令 a= — 1,由(1)可知,函数/(x) =![]() —x 的最小值为f (1)=0,
—x 的最小值为f (1)=0,
∴![]() —x≥0, 即
—x≥0, 即![]() ≥x
≥x
(3)证明:f (x)十ln ≥a+1 恒成立与f (x)十ln x-a-1≥0 f恒成立等价.
令 g(x)=f(x)+lnx-a-1,g(x)=![]() + a(x—1)+ lnx-1,则gˊ(x) =
+ a(x—1)+ lnx-1,则gˊ(x) =![]() +
+![]() +a.
+a.
当a≥—2时,gˊ(x) = ![]() 十
十![]() 十a≥x十
十a≥x十![]() 十a≥
十a≥![]() +a = a十2≥0,(或令φ(x) =
+a = a十2≥0,(或令φ(x) = ![]() 十
十![]() ,则φˊx) =
,则φˊx) = ![]() —
—![]() 在[1,十∞)上递增,∴φˊ (x)在[1,十∞)上递增,∴φ(x) ≥φ(1) = 2,
在[1,十∞)上递增,∴φˊ (x)在[1,十∞)上递增,∴φ(x) ≥φ(1) = 2,
∴gˊ(x) ≥0).
∴g(x)在区间[1,十∞)上单调递增,
∴g(x) ≥g(1)=0,
∴ f(x)十ln x≥a+1 恒成立


科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )
A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+ ![]() )=2
)=2 ![]() .
.
(1)写出C1的普通方程和C2的直角坐标方程;
(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. (Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求 ![]() 的值.
的值.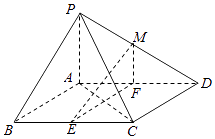
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)等比数列{bn}满足:b1=a1 , b2=a2﹣1,若数列cn=anbn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,a1=1,2Sn=(n+1)an , 若关于正整数n的不等式an2﹣tan≤2t2的解集中的整数解有两个,则正实数T的取值范围为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com